( 嘉兴学院 建筑工程学院 嘉兴 314001 )
【摘要】本文将高速列车作用下的弹性支座简支梁进行简化,以匀速运动的质量弹簧模型通过弹性支承的简支梁为模型,以车桥振动理论作为依据,通过古典车桥耦合问题的分析方法,推导得出模型过桥时的解析解,借助于逐步积分法编制了Matlab数值分析程序。通过数值计算,分析计算阶数、行车速度、支座刚度对车桥动力响应的影响。得出研究结论,对实际工程提供一定的参考。
【关键词】:车桥耦合 弹性支座 质量-弹簧模型
【项目名称】嘉兴学院大学生科技训练项目
Influence of support elasticity on dynamic response of axle system
WangCheng、LiuDejun、BianQinnan
(Jiaxing University, College of Civil Engineering and architectural, Jiaxing 314001 )
Abstract:This article under the action of high-speed trains is to simplify the simply supported beam with elastic support, the quality of motion at a constant speed spring model beam with elastic support for the model, with axle vibration theory as the basis, through the analysis of classical vehicle-bridge problem method, derived the analytical solution of the model bridge, Matlab numerical analysis program is compiled by using step-by-step integration method. Through numerical calculation, the influence of order, driving speed and bearing stiffness on dynamic response of axle is analyzed. The research conclusion is drawn, which provides some reference for the practical project.
Key words: Vehicle bridge action Elastic support Mass-bridge model
0 引言
车辆通过桥梁时将引起桥梁结构的振动,而桥梁的振动又反过来影响车辆的振动,这种车辆与桥梁之间振动耦合的问题已进行了一百多年的研究,研究成果在桥梁设计、维护和控制中起着重要的作用[1]。但大多的研究均假定桥梁两端支承在刚性支座上的,实际上目前广泛应用的橡胶支座存在弹性变形,然而考虑支座弹性的车桥耦合振动的研究还很少。研究表明,当弹性荷载与梁抗弯刚度比值不同时,弹性支撑对梁的振动产生明显影响。同时,不同阶数的模型对桥梁挠度的变化也产生了不同影响,在实际的工作中,只需要采用较大阶数的模型进行研究。
1 梁桥的振动分析理论
桥梁与车辆的相互作用的分析,桥梁的分析理论有如下几种:
Timoshenko理论:在假定平截面的基础上,同时考虑了转动惯量和剪切变形的影响。横向的剪切变形的影响需要考虑,适用于高跨比较大的深梁。
Euler-Bernoulli理论:首先是平截面假定,即假定初始与桥梁轴线垂直的平面,变形后还与桥梁轴线垂直,忽略剪切变形以及转动惯量,对于分析高跨比较小的桥梁较为合理。
实际的工程应用当中,桥梁大部分都是高跨比较小的细长的梁,桥梁在荷载作用下的变形也以弯曲为主,转动惯量的影响和剪切变形的影响一样都很小,所以采用Euler-Bernoulli梁模型理论,能较好的满足计算精度,并且可以简化计算分析。所以本文将采[]用Euler-Bernoulli梁理论。
1.1 弹性支承简支梁的弯曲自由振动
1.1.1 梁桥的振动偏微分方程
如图1-1所示的变截面简支梁,假定此梁的抗弯刚度EI(x)和单位长度质量m(x)沿梁长度方向任意变化,作用在梁上的荷载p(x,t)和横向变位y(x,t)均为随坐标x和时间t连续变化的函数。
.jpg)
这就是简支梁无阻尼弯曲自由振动的偏微分方程,当满足如下边界条件时即为弹性支承简支梁的无阻尼自振偏微分方程[3]。方程的解需要满足在简支梁始端和末端的边界条件,弹性支承简支梁的边界条件为:
.jpg)
桥梁在振动的过程中会受到阻尼的影响,阻尼有两种形式的粘滞阻尼,分为外阻尼和抵抗应变速度的内阻尼,外阻尼引起的阻尼力与桥梁的振动速度成正比,有:
.jpg)
通常假定内阻尼力和应变的速度成正比,根据Euler-Bernoulli的平截面假定,可得弯矩在内阻尼的影响下有如下关系式:
.jpg)
已考虑内阻尼和外阻尼的作用。
1.1.2 弹性支承简支梁弯曲自由振动分析
在给定桥梁的跨度和支座的刚度比条件下,可以计算出频率参数,代入振型函数就能绘制出各阶振型的图像。振型函数由正弦项和余弦项组成,支座的刚度的改变对余弦项的影响较大,因此振动的形态有一定的改变,当刚度比较小的时候,如下图1-2所示支座接近于刚性的时候,各阶振型与刚性支座时没有差别,且幅值均为1。 当支座的刚度减小时,如刚度比增大到时,对应的振型低阶部分没有明显的变化,振动的幅值接近1,高阶部分已经产生明显的变化,与此同时各阶振型的幅值都有一定程度的增大,不同支座的刚度对各阶幅值的影响情况不同,例如刚度比为100时,对5阶振型的影响程度大于10阶振型,所以对弹性支承简支梁的动力分析,振型阶数的选取显的尤为重要。
1.2 弹性支座梁受迫振动求解
1.2.1 无阻尼受迫振动求解
.jpg)
该常微分方程的各阶振型相互独立,方程的解由一个通解和一个特解组成,设方程的特解为,将其代入(2-43)可以得到:
.jpg)
当有多个移动荷载时,广义坐标可以利用叠加原理得到,其表达式为:
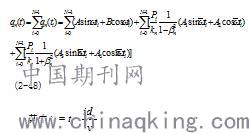
求解多个移动荷载作用下的弹性支承简支梁任意一点的竖向位移时,可以先用叠加原理求的各阶广义坐标,然后根据振型叠加法求算任意一点的竖向位移。
由于弹性支承简支梁的振型函数与刚度比有关系,所以支座刚度的改变会改变广义质量和广义刚度,不同的支座刚度对广义质量产生的影响不同。
2 质量弹簧模型作用弹性支座梁的动力响应
一般情况下,铁路和公路上形式的车辆都会装有弹簧装置和阻尼装置,这些装置不仅可以减轻车辆对桥梁的冲击作用,也可以改变车辆的动力性能,影响到旅客的舒适程度。在本章中将车辆简化为质量弹簧模型通过弹性支承梁来研究车桥的动力响应。首先建立模型振动的运动微分方程,将其与弹性支承简支梁振动的微分方程根据轮对与桥梁的接触关系联系在一起,运用振型分解法对方程进行解耦,最后进行数值分析。
2.1 单个质量弹簧模型
质量弹簧模型通过弹性支承简支梁,移动荷载是质量为的轮对,簧上质量块,刚度为的弹簧和阻尼系数为的阻尼器组成的运动体系。假定质量弹簧模型在移动的过程中,不脱离梁体,所以轮对的位移与梁体的位移相同为y(x,t),簧上质量块的竖向位移是Z(t)。以上各部分组成的计算模型如图2-1所示:
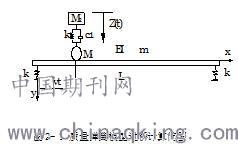
由以上假定可知,车辆的模型由两部分组成,一部分是由刚度的弹簧支承的跳动质量,另一部分是与梁体保持接触的不跳动质量。本文只研究简支梁的竖向振动,不考虑质量弹簧模型加速度引起的桥梁轴向的振动,假定模型以恒定的速度v过桥。
2.2逐步积分法
逐步积分发是采用一系列的时间步长计算结构的反应,一般情况下取为等步长,在每个时间步长的起点和终点建立动平衡关系,根据假定的反应机理,近似计算步长内的不平衡。每一时间步长的初始条件都由前一步长的终点条件确定,也就是说在给定整个系统的初始条件后,就可以根据逐步的动平衡关系求得整个系统的反应,时变特性可以由一系列相继改变的时不变体系进行逼近。由于车桥系统中,车辆的运动性质,广义质量、广义阻尼、广义刚度都在不断变化,准确求解应该在时间步长内用迭代法计算,来满足时段的动平衡关系。假如时间步长足够短,就可以用两点之间的斜率进行近似计算。本文将采用法进行求解。根据上述理论,编制计算程序来计算弹性支承简支梁在质量弹簧模型作用下的动力响应。
3 简支梁动力响应参数分析
根据前述理论分析,我们用Matlab编制了数值计算程序,对弹性支承简支梁在质量弹簧模型(M-K模型)作用下的动力响应进行求解。研究质量弹簧模型过桥参数不同时桥梁的动力响应情况。对于计算阶数、行车速度等影响我们采用单个质量弹簧模型进行研究。
桥梁支座刚度的不同,会影响简支梁的固有频率,下面将给出支座刚度变化时,上述计算简支梁前四阶自振频率的变化情况。
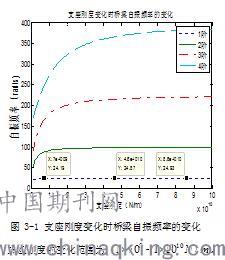
从图3-1中可以看出各阶固有频率随支座刚度的增加有不同程度的增加,阶数越小,随着刚度的增加该阶自振频率越先稳定,一阶固有频率稳定的最快,稳定后随支座刚度的增加,一阶固有频率缓慢增加。各阶自振频率收敛于刚性支座(支座的刚度无穷大)时候的固有频率。刚度变化对低阶自振频率影响较小,高阶自振频率影响较大。
3.1 单个质量弹簧模型简支梁动力响应分析
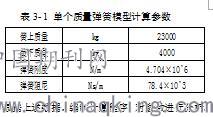
本节将采用质量弹簧模型,分析单个质量弹簧模型过桥时,弹性支承简支梁的动力响应[7],质量弹簧模型的计算参数参数如表3-1所示:
3.1.1 计算阶数的影响
运用振型叠加法计算简支梁的动力响应的时候,振型函数的阶数将影响计算精度,现分析阶数对计算精度的影响。分析中桥墩和地基土层的刚度不考虑,桥梁的支座选取为普通橡胶支座,支座的竖向刚度:
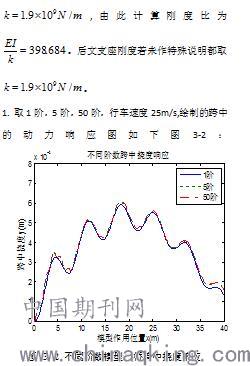
从图3-2中可以看出,跨中产生最大挠度时模型并没有作用在跨中,而是在模型到达跨中之前就达到最大值。计算阶数取1,5,50阶的挠度形态基本一致,前5阶的计算结果与前50阶计算结果基本吻合,所以对于挠度的分析,取前5阶振型即可满足要求。
2. 取1阶,5阶,50阶绘制簧上质量随模型的动力响应图如图3-3所示。
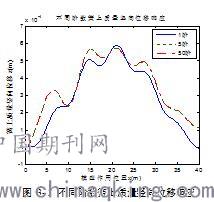
如图3-3,簧上质量竖向位在模型到达跨中附近时出现最大值,5阶振型与50阶振型相符合,取前5阶振型可以基本满足其计算精度。
3. 计算阶数对精度的影响:
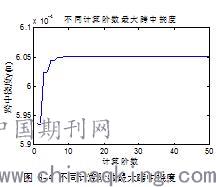
为了分析计算阶数对精度的影响情况,取车速25m/s模型过桥,绘制模型跨中动力响应最大值随计算阶数的变化情况,根据这些图像,找到能满足计算精度的计算阶数。
下图3-4为最大跨中挠度随计算阶数的变化情况,可以看出,动挠度的计算精度随计算阶数的收敛较快,取前10阶计算即可得到较为精确的动挠度响应。
从以上各图的分析中可以看出,虽然弹性支承简支梁作为分布参数体系,有无限多个自由度,但对桥梁动力响应影响较大的是前面几阶振动形态,也就是说桥梁的振动以前面几阶振型为主,高阶振型对动力响应的影响不大。这可以用分布体系振动理论解释:各阶振型的广义质量和广义刚度不同,各阶振型对结构整体振动贡献不一样,工程实际中,只需要考虑对整体振动影响较大的几阶振型,就能得到符合要求的计算结果。模型过桥时,对动内力的分析要适当的计入高阶振型的影响,这与以往分析中得到的结论—高阶振型对位移贡献不大,对弯矩贡献稍大,对剪力的影响更大是相吻合的。在接下来的参数分析中,对位移、速度、加速度等将采用前15阶振型进行分析,对于动内力的分析高阶成分对其影响很大,由以上分析可以看出,考虑前40阶振型的动内力,足够反应桥梁动内力的较为真实的状态。所以对于动力响应取前40阶振型进行分析,对于工程实际来讲,精度满足要求。
4 结论
根据理论分析和实验结果分析得出以下结论:
1.弹性支座梁不同于刚性支承的简支梁,支座刚度的变化,简支梁的基频已经改变,随着支座刚度的降低,简支梁的各阶自振圆频率有不同程度的降低,阶数越低支座刚度对自振圆频率的影响越小。
2.弹性支座梁的广义质量与刚性支座不同,刚性简支梁广义质量随阶数的变化基本稳定,弹性支座梁广义质量在6-10阶会有一个峰值,而后才随着阶数稳定。
3.运用振型叠加法对质量弹簧模型作用下的简支梁动力反应进行分析,弹性支座梁的振动以前几阶振型为主。对于挠度响应一般取低前五阶即可;动内力收敛较慢,应计入较多振型,一般取40阶振型即可满足精度要求;加速度级数在10阶后即已收敛,加速度取前15阶振型可满足精度要求。
参考文献
[1] 肖新标,沈火明. 3种车桥耦合振动分析模型的比较研究[J]. 西南交通大学学报. 2004, 39(2): 172-175.
[2] Yau J D, Wu Y S, Yang Y B. Impact response of bridges with elastic bearings to moving loads [J]. Journal of Sound and Vibration. 2001, 248(1): 9-30.
[3] Yang Y B, Lin C L, Yau J D, et al. Mechanism of resonance and cancellation for train-induced vibrations on bridges with elastic bearings[J]. Journal of Sound and Vibration. 2004, 269(1–2): 345-360.
[4]钱长照,李寅磊,刘扬. 弹性支撑梁在移动荷载作用下的响应分析[J]. 动力学与控制学报. 2011, 9(2): 162-166.
[5] 刘元志. 支座特性对承受高速移动列车荷载简支桥梁动力响应的影响分析[J]. 公路交通科技:应用技术版. 2013, 9(7): 285-287.
[6] Frýba L. A rough assessment of railway bridges for high speed trains[J]. Engineering Structures. 2001, 23(5): 548-556.
[7] 陆建飞,吴嘉彬,沙萱. 系列移动荷载下周期性弹性支撑连续梁的共振及消振效应[J]. 河海大学学报:自然科学版. 2016, 44(2): 141-148.
论文作者:王程、刘德军、边钦楠
论文发表刊物:《科学与技术》2019年第08期
论文发表时间:2019/9/10
标签:支座论文; 刚度论文; 模型论文; 弹性论文; 桥梁论文; 质量论文; 阻尼论文; 《科学与技术》2019年第08期论文;
