摘 要:由于应用惠更斯-菲涅耳积分解决衍射问题比较复杂,菲涅耳提出了一种简便方法---菲涅耳半波带法。本文中主要介绍菲涅耳半波带法原理,并探讨用菲涅耳半波带法处理非光轴上点光强以及半波带数k值等相关问题,分析它在单缝衍射、光栅衍射和波带片中的应用。
关键词:菲涅耳半波带法 惠更斯-菲涅耳原理 半波带数
一直以来,衍射现象的研究在光学中占有十分重要的地位,菲涅耳把惠更斯提出的次波概念和杨氏提出的干涉原理结合起来,建立了惠更斯-菲涅耳原理。它可以解释和描述光通过各种障碍物时所产生的衍射现象,定量地研究衍射问题,但积分常常比较复杂。菲涅耳提出了一种简便方法---菲涅耳半波带法,它能够定性地分析各种衍射现象,使所处理的问题形象,直观,而且过程非常简单。
一、菲涅耳半波带法介绍
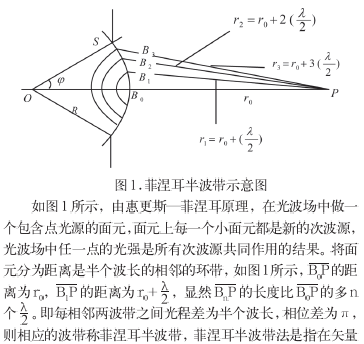
合成时把每一个半波带作为一个整体来考虑。
二、菲涅耳半波带法的探讨
当半波带面恰好分成n个完整的半波带时,利用菲涅耳半波带法直接得光轴上点光强。若狭缝平面的波前面不能恰好分成n个完整的半波带,这时需要将每个半波带进一步划分。
对于第一个半波带分成m个更窄的环带,振动的矢量可由图2a来表示。
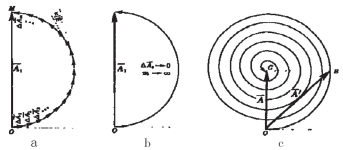
图2.振动矢量图
如图2a所示,若不考虑倾斜因子K(θ)的影响,能很好的将这个半波带分成无数个子带,并且随着每一个子带的叠加,逐渐形成一个误差极小的半圆,如图2b所示。同理对于所有的半波带来说,每增加一个半波带就增加一个半圆,而且半径随着波带的增加而减小,如图2c所示,A就是无数个半波带合成的振幅。
三、菲涅耳半波带法的应用
1.理论应用
(1)单缝中应用
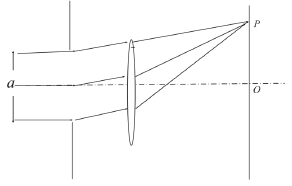
图3.夫琅禾费衍射
如图3所示,研究单缝问题一个重要的方面就是怎么得出明纹公式,而应用菲涅耳半波带法可以很好地方便地得出公式,现在最大的问题是光程差能不能满足半波带的要求,即最大光程差d等于几个半波长,当最大光程差为半波长的偶数倍时,相干加强,为明纹;当最大光程差为半波长的奇
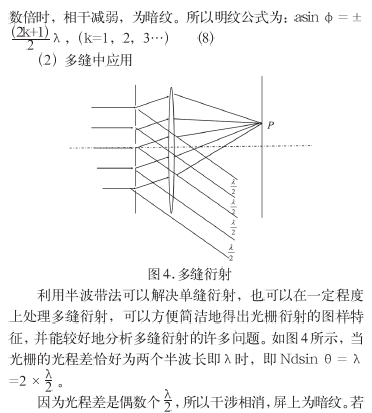

菲涅耳半波带法不仅可以用来处理单缝衍射,而且可以用来处理光栅衍射。
2.实际应用
菲涅耳半波带法在实际应用方面相当广泛。例如,利用菲涅耳半波带法制成的波带片是在19世纪70年代首先制成的。由于当时制作工艺上的困难,科学技术上的困难,社会等原因,人们一直以来将菲涅耳半波带片忘记了,很长时间以来没有得到很好的应用。直到现在,人们对它有了新的认识,特别是随着激光和全息术的发展,近年来才使得它广泛应用于很多关键、重要的领域。菲涅耳透镜也是利用菲涅耳半波带法制成的,它也有许多优点,在现实生活中有广泛的应用。
总之,菲涅耳半波带法是一种简便的方法,可以定性地分析很多问题,并且能突出相关的概念,形象直观,但也有一定的局限性,尤其在定量上我们不能对它要求过高。
论文作者:陈 乾
论文发表刊物:《素质教育》2014年1月第144期供稿
论文发表时间:2014-5-5
标签:光程论文; 惠更斯论文; 波带片论文; 如图论文; 所示论文; 很好论文; 波长论文; 《素质教育》2014年1月第144期供稿论文;
