(成都理工大学工程技术学院,四川 乐山 614000)
摘要:在实际工程领域中,相当部分的脆性材料总是不可避免的存在着裂纹或是缺陷。在实际环境中材料的受力往往是相当复杂的。基于ABAQUS平台的裂纹仿真软件,它具有简单易用的特点。通过算例分析验证表明,该软件的计算结果具有较高的精度,完全可以用于实际工程问题的计算,通过分析验证表明该软件的设计是成功的。此外,今后可以在它的基础上进行更多功能扩展,从而使它拥有分析更为复杂问题的能力。
关键词:裂纹;应力强度因子;断裂力学;ABAQUS
引言
材料在成型和加工过程中在其内部造成了很多缺陷,而其破坏正好均源于构件内部的微小裂纹,所以研究带裂纹的物体力学性能具有十分重要的意义。

图1存在于岩石和混凝土地面中的裂缝
1920年, Griffith[1-2]提出了在材料中存在裂纹的设想,而从Irwin[]3-4]在1957年提出了应力强度因子以及其后形成的断裂韧度的概念后,断裂力学理论出现了重大的突破,奠定了线弹性断裂力学的基础。
1基本原理
近年来以数值分析为基础的手段来解决断裂力学相关问题的技术得到了广泛的发展应用,并且不断的调整完善。该技术在一定程度上较好的克服了实验条件下的不足。对于线弹性断裂力学而言,裂尖区域的位移场、应力、应变场由应力强度因子决定,故而通过有限元计算的结果来得到具体的应力强度因子的值是线弹性断裂力学中用有限元法的基本要求。
1.1 ABAQUS求解裂纹尖端的应力强度因子
传统的有限元在计算裂纹尖端的应力强度因子的时候,无可避免地遇到裂尖复杂应力场和位移场的计算,J积分则可以完全避免这种复杂的处理过程。
为了计算二维情况下的J积分,ABAQUS定义了围绕裂纹尖端由单元组成的环形的积分域,如下图所示。
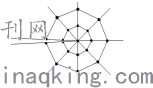
图2 ABAQUS中围线的定义
ABAQUS在计算围线积分时,采用的是先计算出围线上面所取的若干个离散点处J积分值,然后乘以每个点对应的加权值后,所有点相加来近似地求解出围线积分,即J积分的值和,进而得到复合裂纹的应力强度因子和。
2两条共线裂纹应力强度因子的算例分析
2.1共线双裂纹在压缩荷载作用下应力强度因子的解析解
有许多学者对含有裂纹的无限大板,裂纹尖端的应力强度因子进行了研究。Zhu Z M[5] 等从理论和实验两个方面都做了详细的研究与探讨。基于前人的研究结果,Zhu Z M 给出了共线裂纹的应力函数及其应力强度因子的基本公式,并就共线双裂纹问题进行了研究,给出了裂纹应力强度因子精确的解析解。
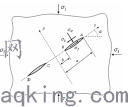
图3压缩载荷作用下的含有共线双裂纹的无限大板
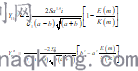
2.2 ABAQUS计算共线裂纹应力强度因子
为验证ABAQUS软件计算应力强度因子的准确性,现取以15度为梯度的倾角进行验证性运算,即取角度为:=0,15,30,45,60,75,90;同时定义a=5mm,b=15mm;=0.5。将结果和解析解进行比较,对比结果如图4、5所示。
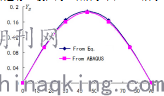
图4 理论值与计算值比较(B)
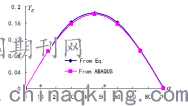
图5理论值与计算值比较(A)
由上面的图表分析知:很明显基于ABAQUS的数值模拟技术在计算简单裂纹的应力强度因子上是可靠的。
3基于ABAQUS的复杂裂纹应力强度因子算例
3.1 V型裂纹应力强度因子解析解
关于对称V型分支裂纹的应力强度因子问题,Yavuz等[6]从理论上通过裂纹线上的边缘位错分配法分析了在无限大板中的多种相互作用的裂纹问题。在此根据Yavuz等的理论研究,作者通过ABAQUS来对Yavuz的理论研究进行了对比,探究基于该软件研究复杂裂纹的可行性。
3.2 ABAQUS计算V型裂纹应力强度因子
下面讨论如图所示的V裂纹裂尖应力强度因子问题。取=,的值依次取为0.1,0.2,0.5,1.0,1.5,2,5,10,单轴拉伸荷载=1。结合Yavuz所给出的理论结果,作者依据Abaqus进行了相同情况下的数值模拟,列举了A,C,D,F四点的应力强度因子
KⅠ,KⅡ。
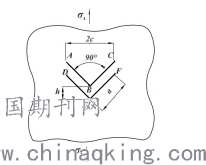
图6 含两条V型裂纹的无限大板模型

图7 理论值与计算值比较
对比Yavuz所给出的值,可以发现利用Abaqus所计算的结果和理论结果具有很高的吻合性。
4 结论与展望
裂纹本身形态的复杂多样性以及其所处应力环境的复杂性给研究带来了相当大的困难。本文采用理论、数值模拟相结合的方法对含裂纹脆性材料的破坏准则进行了研究。
结果表明基于ABAQUS平台的裂纹仿真软件,它具有简单易用的特点。通过算例分析验证表明,该软件的计算结果具有较高的精度,可以用于实际工程问题的计算。
参考文献
[1]Griffith A.A. The Phenomena of ruptures and flow in solids [J].Phil.Trans,1920,
Ser.A:163-198.
论文作者:汪波
论文发表刊物:《新材料.新装饰》2018年3月下
论文发表时间:2018/9/11
标签:裂纹论文; 应力论文; 因子论文; 强度论文; 力学论文; 积分论文; 无限大论文; 《新材料.新装饰》2018年3月下论文;
