摘要:利用SCADA系统中主变开关的负荷数据和营销系统中用户的容量数据,求解不同用户类别的负载率水平。使用用户容量和开关负荷数据构建多元一次方程组,利用最小二乘法、K均值聚类算法和二叉树深度遍历的思想,将总的方程组拆分得到许多较小单元的方程组,从而计算得到总体负载率的范围。
关键词:SCADA;负载率;最小二乘法;K-均值;二叉树深度遍历
一、引言
利用SCADA系统中开关的负荷数据和营销系统中用户的容量数据,并将用户按照用电特性分为四类:居民用电、非工业、商业和工业,求解不同用电类别用户的负载率情况。传统的方法主要有最小二乘法等,但考虑到不同开关可具有不同用电类别的用户,开关容量存在一定的误差等因素,构建了以下基于聚类-二叉树的负载率计算模型,并通过数据实验进行分析和验证。
二、聚类-二叉树模型
1.k均值聚类算法
k均值算法的基本思想是:通过迭代寻找k个聚类的一种划分方案,使得用这k个聚类的均值来代表相应各类样本时所得的总体误差最小。其代价函数是:

k均值算法的处理过程:
1)随机选取k个中心点
2)遍历所有数据,将每个数据划分到最近的中心点
3)计算每个聚类的平均值,并作为新的中心点
4)重复2)-3),直到这k个中心点不再发生变化,或执行了足够多的迭代
2.k均值聚类-二叉树模型
为了求解居民用电、非工业、商业和工业这四类用电类别的负载率情况,将模型抽象为一个多元线性回归模型,但此模型有三个特点:
线性方程的元不确定
线性方程的数量较多
部分线性方程的变量值存在统计误差
因此不能使用多元线性回归的常用方法—最小二乘法,直接对所有线性方程进行计算,这样会导致较大的误差。针对数量较多的开关,目标能够得到解的误差较小的分组,因此模型的主要步骤为:
1)使用最小二乘法计算不同用电类别的负载率,并计算根据结果负载率得到的开关负荷值与实际值的相对误差 ,其中
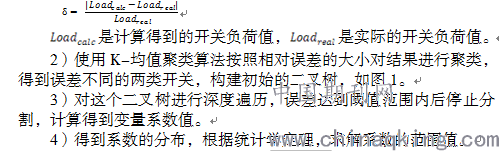
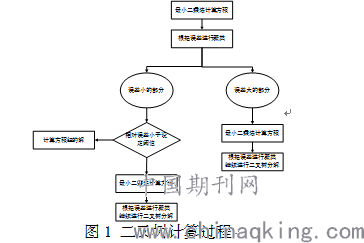
三、实验分析
选择地区变电站中的119条出线开关容量负荷数据进行实验。
1.按照用电性质构成分类
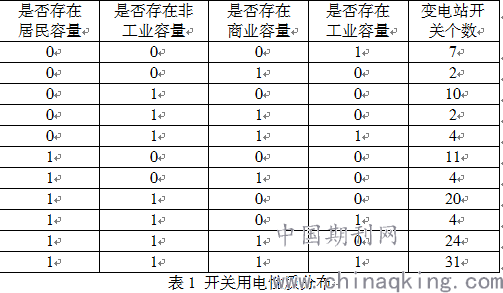
2.四种用电类别用户负载率系数分布
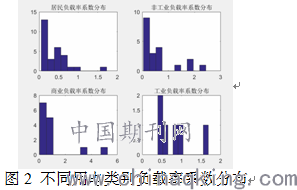
其中,横轴表示负载率系数,纵轴表示开关频数
3.参数估计
选取置信水平为80%,即 1.28
负载率系数的区间估计值为:
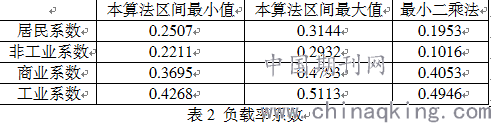
由表2可知,用户负载率系数中,工业最大,商业次之,非工业再次,居民负载率系数最小。本文算法得到的系数区间和最小二乘法得到的系数值中,除了非工业有较大的差距,其他结果基本相似。
4.结果评价
●使用holdout方法选择测试数据,留出比例为20%
●相对误差分布
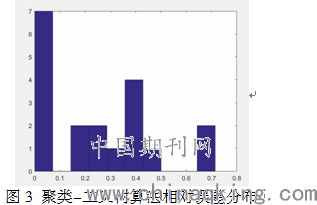
本文算法与最小二乘法相对误差结果比较

由表3和图3的结果可知,聚类-二叉树算法相对于最小二乘法,平均行对误差减小,而且相对误差集中于误差较小的区域,表明聚类-二叉树算法相对与最小二乘法而言负载率系数结果更加精确。
四、结论
本文通过分析负载率计算模型的数据特点,建立了基于k均值聚类-二叉树的负载率计算模型,并选取部分开关数据进行实验,计算不同用电类别负载率系数的区间。最后将本文算法结果和最小二乘法得到的结果进行比较,得出了本文算法相对与最小二乘法相对误差更小的结论。
参考文献:
[1] 李志永,陈立潮,张英俊。基于特征空间聚类的二叉树支持向量机分类算法[J]。计算机与数字工程,2010,38(6):32-34
[2] 荣雅君,张田田,王娜,等。改进灰色理论与最小二乘法在中长期电力负荷预测中的应用。中国高等学校电力系统及其自动化专业学术年会,2011
[3] 贺仁亚,程乾生,孙喜晨。属性均值聚类二叉树及其在人脸识别中的应用。《北京大学学报(自然科学版)》,2002,38(5):616-621
论文作者:陈晨,万顺,陈家静
论文发表刊物:《电力设备》2017年第18期
论文发表时间:2017/11/6
标签:负载论文; 乘法论文; 误差论文; 小二论文; 算法论文; 系数论文; 模型论文; 《电力设备》2017年第18期论文;
