摘要：为了评估铁路连续刚构桥在罕遇地震作用下抗震性能，利用大型有限元程序Midas Civil建立桥梁三维有限元模型，考虑墩柱的非线性特性进行罕遇地震作用下大桥的非线性时程分析。结果表明：大桥主墩底部区域在罕遇作用下顺桥向、横桥向均进入塑性，而边墩底部区域顺桥向没有进入塑性，横桥向则进入塑性。并且所有墩柱的位移延性系数满足规范要求，表明墩柱的延性能力足够。
关键词：罕遇地震；连续刚构桥；有限元；弹塑性分析；地震响应
1.引言
高墩大跨径连续刚构桥的抗震性能评估既是桥梁抗震研究的热点又是抗震研究的难点，国内外很多学者对这一问题进行了研究。刘璐等[1]结合某轨道交通的高架桥梁工程，采用纤维模型，分析了该桥在地震作用下的受力状态，分析表明：该桥制动墩墩底钢筋在给定地震时程波作用下发生屈服，桥墩进入塑性状态，但非线性位移延性比满足规范要求；谭冠生[2]建立基于纤维模型有限元法的非线性数值分析模型，研究某高墩大跨连续刚构桥在罕遇地震作用下的动力响应。陈星烨[3]基于能力设计原理，对某连续刚构梁桥进行弹塑性地震响应分析。分别考虑桩-土作用与忽略桩-土作用建立有限元计算模型，采用刚度退化三线型模型，计算出该桥桥墩与桩恢复力计算模型的特征参数，在设防烈度与罕遇地震作用下，对其进行弹塑性地震反应非线性计算。李林[4]利用大型结构分析软件建立了空心薄壁高墩大跨T形刚构桥的空间抗震有限元模型，运用非线性动态时程反应方法进行了高烈度地震区罕遇地震作用下的弹塑性地震反应计算，并与线性时程法和反应谱法的计算结果进行了对比。何钦象[5]根据高墩大跨径连续刚构桥特点提出了一种适合于其弹塑性地震响应的分析方法，利用提出的塑性铰单元和已有的有限元程序，实现了对罕遇地震作用下桥梁结构的地震响应模拟。
本文以实际铁路连续刚构桥为工程背景，研究了罕遇地震作用下连续刚构桥的弹塑性动力响应和抗震性能，旨在为该类桥梁的抗震设计提供指导。
2.工程概况及有限元模拟
2.1工程概况
连续刚构桥主桥采用（40+72+40）m连续刚构结构形式。主桥主梁为预应力混凝土结构，采用单箱单室变高度箱形截面，主跨跨中及边支点处梁高为3.2m，中支点处梁高为5.2m，梁高按圆曲线变化。主桥桥墩15#、18#采用圆端形空心墩，16#、17#采用矩形空心墩，墩高分别为59m、54.5m、50.8m和59.8m。支座采用球形支座，在边支点沿横向设2个支座，边支点支座吨位5000kN，中支点无支座。主桥位于抗震设防烈度Ⅶ度区域，地震动峰值加速度0.15g，地震动反应谱特征周期为0.45s。主桥立面图如图1所示：
.png)
图1 主桥立面图
.png)
图2 全桥有限元模型图
2.2 有限元模型
大桥采用midas civil有限元计算分析程序，根据桥梁结构的总体构造布置，建立了结构动力特性和地震反应分析的三维有限元模型。全桥主梁、墩模拟为考虑了剪切变形的三维弹性Timoshenko梁单元。在罕遇地震作用下，因为墩身很可能进入塑性，所以需用弹塑性梁柱单元模拟，主梁仍模拟为考虑了剪切变形的三维弹性Timoshenko梁单元。承台主要作为质量单元参与响应贡献，所以承台也作为梁单元处理，但质量仍然精确反映。全桥有限元模型见图2。
2.2.1 钢筋和混凝土模拟
本次研究钢筋纤维本构采用能考虑“Bauschinger”效应的修正梅内戈托与平托模型（Modified Menegotto & Pinto Steel Model）如图3。
.png)
图3 修正的Menegotto-Pinto模型
.png)
图4 mander模型
图中，e为钢纤维的应变；s为钢纤维的应力；（er，sr）为卸载点位置，在弹性状态时假定为（0，0）；（e0，s0）：定义当前加载或卸载路径的两个渐近线的交点；b指刚度折减率；R0，a1，a2常数（决定曲线状态的参数，程序使用了试验获得的优化值）；x指在加载/卸载的方向上最大应变与e0的差（绝对值），最大应变的初始值假定与±（Fy/E）相同。
混凝土纤维采用1988年Mander等针对横向约束混凝土提出的本构模型如图4。对于约束混凝土本构，因为本桥墩身截面形式主要有圆端实心和圆端中空两种，而两种截面箍筋对于混凝土的约束效果不尽相同，所以应该分别考虑。
3.地震动输入选择
3.1场地反应谱
根据《中国地震动反应谱特征周期区划图》和本桥《工程地质勘察报告》，项目经过地区的地震抗震设防烈度为7度，设计基本地震动峰加速度0.15g，场地类别为Ⅱ类，频谱特征周期为0.45s。由《铁路工程抗震设计规范》GB50111-2006（2009年版）[6] 7.1.4条。本桥地震作用分析只考虑水平向地震作用，常遇地震作用下水平向加速度反应谱曲线（纵坐标单位 ）见图5。
.png)
图5 地震水平向加速度反应谱曲线
3.2地震动合成
采用拟合目标函数的三角级数叠加法合成人工地震波。地震波应该满足以下三个条件：（1）频谱特性，即场地条件和设计分组地震确定，满足场地特征周期Tg接近或相同；（2）加速度有效峰值；（3）持续时间。
为考虑地震动的随机性，设计加速度时程不得少于三组，且应保证任意两组间同方向时程的相关系数ρ的绝对值小于0.1。对于罕遇地震，拟采用以下三条人工波对结构进行抗震分析：
.png)
A波
.png)
B波
.png)
C波
图6 人工罕遇地震动
4.地震响应分析
4.1桥墩响应
4.1.1 桥墩响应汇总
地震荷载工况按方向主要分为顺桥向及横桥向，其墩柱内力响应见表1、2所示。
表1 恒载+活载+顺桥向地震激励
.png)
表2 恒载+活载+横桥向地震激励
.png)
通过A、B、C三波比较可知，对于不同的墩柱甚至同一墩柱不同的内力响应峰值，并不是一定为同一地震波，比如主墩顺桥向弯矩在B波激励下达到最大，但边墩顺桥向弯矩在A波激励下达到最大，所以应该根据最不利原则对于不同的内力选取不同的工况进行验算；主墩在顺桥向地震激励下，除了墩底区域截面弯矩较大外，墩顶也出现了弯矩较大的区域，所以对于刚构桥梁，除了考虑墩底在大震下可能进入塑性外，还必须考虑墩顶区域进入塑性后整个墩身结构刚度的变化。
4.1.2 墩柱顺桥向工作状态判定
对于主墩来说，墩底实心圆端截面顺桥向弯矩最大在B波工况二，如图7为主墩底实心圆端区域最不利截面的破坏情况，可见截面混凝土开裂且最外层钢筋在罕遇d地震作用下发生屈服，最大弯矩为1655547 KN*m，其弯矩-曲率曲线如图8有较大的滞回耗能。
.png)
图7主墩实心底截面绕Y轴纵筋图
.png)
图8主墩实心底截面绕Y轴弯矩-曲率曲线
如图9为主墩中空圆端区域最不利截面的破坏情况，可见截面混凝土开裂且最外层钢筋在罕遇地震作用下发生屈服，最大弯矩为1093906 KN*m，其弯矩-曲率曲线如图10比较扁平，说明进入塑性不够充分，耗能有限。
.png)
图9 主墩中空底截面绕Y轴最终纵筋
.png)
图10 主墩中空底截面绕Y轴弯矩-曲率曲线
4.1.3墩柱位移延性验算
参考我国《铁路工程抗震设计规范》GB50111-2006（2009年版）[6]第7.3.3条，钢筋混凝土桥墩在罕遇地震作用下的延性验算应满足下式的要求：
.png)
式中，.png)
——非线性位移延性比；
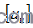——允许非线性位移延性比，取值为4.8；.png)
——桥墩的非线性响应最大位移；.png)
——桥墩的屈服位移；
根据桥墩在实际地震激励下的最大发生位移如表3可知，其中边墩在横桥向方向的位移延性比最大为2.06，但仍小于《铁路工程抗震设计规范》GB50111-2006（2009年版）[6]所要求的4.8，所以墩身位移延性需求均满足规范要求。
表3 墩身位移延性比验算
.png)
需要说明的是：该桥在罕遇地震下，主墩柱在顺桥向、横桥向两个方向均处于塑性阶段工作范围，所以对于主墩两个方向上的抗剪设计值，主墩基础两个方向上的弯矩、剪力和轴力设计值均应采用能力保护原则来进行计算，也就是由墩底截面的抗弯承载能力而不是地震响应来得到。
5.结论
本文通过罕遇地震作用下的弹塑性时程分析，利用大型有限元程序Midas Civil建立桥梁三维有限元模型，考虑墩柱的非线性特性进行罕遇地震作用下大桥的非线性时程分析。主要结论有：
（1）利用大型有限元计算分析程序midas Civil对整桥进行空间模型建立，并考虑施工阶段的内力累积效应及土对桩的影响。（2）考虑墩柱的非线性特性进行设计地震及罕遇地震作用下大桥的非线性时程分析。可知大桥主墩底部区域在罕遇作用下顺桥向、横桥向均进入塑性，而边墩底部区域顺桥向没有进入塑性，横桥向则进入塑性。并且所有墩柱的位移延性系数满足《铁路工程抗震设计规范》GB50111-2006（2009年版）[6]的要求，表明墩柱的延性能力足够。
参考文献：
[1] 刘璐，徐刚，赵川杰，等. 罕遇地震作用下铁路连续梁桥抗震分析[J]. 公路工程，2015（6）：111-113.
[2] 谭冠生. 罕遇地震作用下高墩大跨连续刚构桥地震响应分析[J]. 铁道建筑，2016（6）：27-30.
[3] 陈星烨，颜东煌，刘文浩. 某连续刚构梁桥的弹塑性抗震性能分析[J]. 中外公路，2008（3）：75-81.
[4] 李林. 罕遇地震下空心薄壁高墩大跨T形刚构桥弹塑性地震反应分析[J]. 地震工程学报，2013（1）：56-61.
[5] 何钦象，田小红，宋丹. 高墩大跨径连续刚构桥抗震性能评估[J]. 振动与冲击，2009，28（1）.
[6] 中华人民共和国建设部. 《铁路工程抗震设计规范》GB50111-2006（2009年版）[S]. 北京，2009.
论文作者:熊佳
论文发表刊物:《建筑模拟》2020年第2期
论文发表时间:2020/4/14
标签：塑性论文; 延性论文; 弯矩论文; 截面论文; 位移论文; 模型论文; 桥墩论文; 《建筑模拟》2020年第2期论文;