摘要:船舶下水是船舶建造中很重要的一个过程,而成千上万的船舶在纵向下水过程中难免会有一两艘因计算失误等原因造成发生艉下落与艏下落的不利现象发生,因而及时防患于未然有利于相应损失的减少。本文就此方面提供一种研究的思路供参考,其主要思想就是将 “化尖为曲”。
关键词:艉下落;船舶下水;弧
一、艉下落与艏下落定义
艉下落与艏下落都是船舶在纵向下水中可能会发生的一个不允许发生的情况。艉下落通常发生在船舶下水的第二阶段,指当γVSB<WcSG时(式中V为船舶入水部分的排水体积,Wc为船舶下水重量,SG和SB分别指重心G和浮心B至滑道末端的距离),船以滑道末端为支点而发生的现象,此时反力集中于滑道末端,使船体受到损伤。同理,艏下落通常发生在船舶下水的第四阶段,在下水架前支点离开船台滑道末端时,船未完全浮起,船舶的下水重量仍大于浮力,此时将发生船艏下落现象。
二、减少艉(艏)下落影响必要性
要值得注意的是,本文阐述的主要内容是怎么样做可以减少当船舶发生艉或艏下落时所带来的危害。而不是防止艉或艏下落的发生,因为对此类问题的完善已经具有了许多相应的措施,如:增加滑道水下部分的长度、增加滑道坡度、等待潮水更高时下水等等,这里就不在详细论述了。
虽说当今的计算机模拟技术等已经变得十分成熟已经可以有效地减少船舶发生艉或艏下落的几率,但是,这仍然不能否认船舶发生此类现象的可能性。而一旦船舶发生此类现象的话,一方面,船舶的尾端理论上容易与水底碰撞,发生损害,而在现实上,水底存在大量淤泥,这些淤泥可减缓船舶的尾端与水底碰撞所带来的危害,这一点就不在这里讨论了;另一方面,此时滑道末端由于压力巨大,而受力面积微小(当假设船台为刚体时,受力面积最初只有一条线)所受到的应力非常大,很可能超过钢材的许用应力,导致船舶底端钢材的部分变形甚至破裂,对人力物力时间成本的损耗也是巨大的。因此,防患于未然,想方设法地用较少地成本去维护较多的利益是十分有必要的。
三、减少艉(艏)下落影响的方法
(一)方法的原理
1.假设船台是刚体
以第二阶段为例,假设船台是刚体时,这就意味着当下水架与船台发生碰撞以后,所有的不利因素都会反馈给下水架,进一步地对船舶艉部造成损害,正如上述所述的那样,船舶艉下落之所以会有如此巨大的危害,是因为而在材料力学中,应力集中一般出现在孔槽附近。打个比方,在现实生活中,将一张带孔的纸往两头相背拉扯,最早出现裂纹的地方就在该孔附近。由于此规律的存在,只会使得原本就已经受到破损的船体雪上加霜。因此,使得船台上的最初接触面积增大变得十分重要,增大最初接触面积的一种方法就是在不影响船舶下水或者影响船舶下水较小的前提下,将尖点去掉。
2.假设船台不是刚体
而假设船台不属于刚体时,则意味着当下水架与船台进行碰撞以后,由于力的作用是相互的,船台与下水架二者会相互磨损,而船台经过无限次的磨损以后(这里要说明的是,由于当今计算手段和计算方法先进,二者之间的磨损次数很少出现,甚至不出意外的话连船舶艉或艏下落的现象都不可能出现,但是这里仅仅是寻找合适解甚至最优解的一种假设法),会磨损成对艉或艏下落影响较小的那种光滑形态。这种磨损会随着次数的逐渐增多而在此方面带来有利影响。但是,仅用上述手段去追求该有利影响是需要代价的,代价就是对船体的损害。而这种有利影响可以人为地去获取,就是用其他物品或者机器人为地造成这种“磨损”,即上面提及的去掉船台的尖点。
(二)方法的表述
其方法其实很简单,如图3-1所示,将船台末端的尖角打磨光滑,其斜率由下水方向(向量AB方向)依次增大至正无穷(至竖直方向),其中除最后一点C外处处可导。
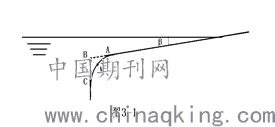
其中虚折线ABC部分代表现在传统船台的尖点,实曲线AMC部分代表现在正常船台,β角为一般情况下船台的倾斜角度(根据船长的情况下从正切值1/12~1/24不等,大船小值,小船大值)。
此外,一方面,图中的曲线AC形状可以根据船舶的长度等因素有许多不同的函数,图中为了图片绘制的方便,就仅仅用一般的弧线进行替代;另一方面AB,BC的距离也有可能随着船舶的许多因素而发生变化。这里仅仅就对这种“化尖为曲”的思路进行定性的表述,至于实际上曲线的样式以及曲线的尺寸等定量的问题还需近一步地进行相关试验与相关研究,这里就不再详细描述了。
四、方法可能会带来的其他影响
(一)正常下水时
第二阶段时,当正常下水时,按照船舶下水的原理,此时γVSB>WcSG,船舶与滑道与滑道仍然贴在一起,此时反作用力(支持力)R所作用的面是一个远大于一条线的一个平面(该平面的长为A或B点到船艉的长度),因此相对于半个船长来说有无AB这一段不会有较大的关系;第三阶段时,在此阶段时,船艉开始上浮,此时正常情况下,船舶底部已经脱离B点(不论B点是船台还是水),因而两者不论有无都没有太多影响;第四阶段时,同第三阶段,二者在正常下水情况下是不会相触碰的。因此,无论有无都没有较大影响。
(二)未能正常下水时
1.增加了滑道的坡度
显然可以从图中看出,其滑道到达A点以后,图形的斜率逐渐增加,这也就意味着滑道坡度逐渐增加。虽然其角度增加后的度数一定会超过标准值(即β角的规范角度),但是这对总的船舶下水起不到什么影响,理由如下:(1)船舶下水中,之所以按照经验规定β角的规范角度是因为防止船舶在整个下水过程中因为速度太快产生各种影响不利影响,而这里只是局部现象;(2)在传统船台上,其角度最后也是要达到90°的,只是区别于设计方案的渐变,大小直接从β在B点突变为90°。相反,一部分的坡度增加,使得浮力增加(即使增加很小),对船舶的下水是具有有利影响的。
2.表面上减少了滑道水下部分的长度
虽说从定义上来看,滑道水下部分的长度减少了|AB|,但这仅仅是表面现象。事实上,毕竟弧AC段对此的影响也应该考虑部分在内,就拿图形ABCM而言,直线AB的长度未必大于弧AM的长度要长,即使确实大于的话相差也不是很大(其中M点为在该设计中,船舶发生艉下落时,最远能到达的船台上的点,其位置根据不同船舶的参数变化而不同)。
五、总结
综上,此方法能有效地减少当船舶发生艉或艏下落时对船舶、下水架和船台的不利影响。虽说其也存在着许多可能会新产生的不利影响,但是很明显地,此类的设计总的来说是利大于弊的。
参考文献
[1]盛振邦,刘应中.船舶原理(上)[M].上海:上海交通大学出版社,2003.
论文作者:邱昕捷
论文发表刊物:《知识-力量》2019年12月61期
论文发表时间:2020/3/26
标签:船台论文; 船舶论文; 下落论文; 滑道论文; 发生论文; 刚体论文; 磨损论文; 《知识-力量》2019年12月61期论文;
