宁夏彭阳第二中学756500
摘要：数学是一门理论性和逻辑性都比较强的学科，对学生的思维能力要求比较高。逆向思维能力就是其中一种比较重要的思维能力表现形式。本文就此展开了讨论，结合实际详细分析了如何在各种题型中，应用逆向思维，寻找解题思路。
关键词：逆向思维；初中数学；解题教学；应用
逆向思维是打破传统思维框架，反其道而行之。培养学生的逆向思维能有效改变学生的思维定式，引导学生从问题入手，寻找解题思路。为此，在初中数学解题教学中，教师应从解题实际入手，将逆向思维的应用方式展示给学生，从而提高学生的逆向思维意识，加快学生解题速度。
一、在函数解题教学中的应用
在函数解题教学的过程中，学生既要抓住题干，了解题目内容，也要理清已知变量、所求变量之间存在的关联。若要应用逆向思维，就要深入了解所有变量之间的内在联系，从问题出发，逆向推导。
例如：(1) 二次函数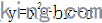
的图像向左平移三个单位，再向上平移2个单位，得二次函数
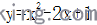的图像，求b、c的值。(2) 将抛物线
先向下平移1个单位，再向左平移3个单位，求平移后的抛物线的解析式。首先，仔细观察两个问题的题设、结论能够发现，它们是互逆的。若要解决这两道题目就结合函数图像平移特点入手。同时，结合抛物线方程能够发现(1) 、(2) 图像的顶点比较容易计算。那么可从顶点坐标平移方面考虑。其中(1)是经过平移后的抛物线，其顶点坐标为(1、0)，那么就能推算出未平移前的顶点坐标为(4、-2)。将(1)的计算方向完全颠倒过来，便能推算出(2)平移后的顶点坐标为(-2、5)。在完成顶点坐标的计算后，就可将(1)、(2)的抛物线方程整理成标准形式，从而计算出最终的结果。对比上述两道题目来说，其解题思路恰好是相反的，正能培养学生的逆向思维，打破学生的传统认知。
二、在几何证明题解题教学中的应用
逆向思维在初中数学解题中的应用也非常广泛。实践证明：利用逆向思维不仅仅能简化解题过程，更能提升解题效率。最重要的是在应用逆向思维解题时，能够点拨学生，使其“守得云开见月明。”而且无论是函数题型，还是几何证明、应用题等题型，逆向思维都有所应用。
例如：如上图1，在△ABC中，AD=AB，∠EBD=∠DBC，求证：AD2=AE·AC。显然，观察这道题能够发现，已知条件并不多，若要证明最终的结果就必须要借助相似三角形。但给出的条件并不充足，无法明确要证明哪两个三角形是相似的。所以要从结论入手，先将AD2=AE·AC进行变形，即AD/AE=AC/AD。结合图形能发现，不存在△ADE、△ACD，那么我们要结合给出的条件，对AD/AE=AC/AD继续变形。已知AD=AB，那么AD/AE=AC/AD可变形为AB/AE=AC/AB。再结合图形分析，发现△ABE、△ABC是存在，且存在相似的可能性。所以我们可尝试证明这两个三角形是否相似。首先，这两个三角形共同顶角∠A。那么我们只需要再找出一个等角即可。其次，AD=AB，那么在△ABD中，∠ABD=∠ADB。因为∠ABD=∠ABE+∠EAD，∠ADB=∠C+∠DBC，所以∠ABE+∠EAD=∠C+∠DBC，其中∠EBD=∠DBC，因而∠ABE=∠C。因为∠ABE=∠C，∠A=∠A，所以△ABE与△ACB相似。从中能够发现，应用逆向思维更能发现解题思路。尤其是在一些已知条件与所求条件关联性不强的条件下，逆向思维更有助于学生快速解题。为此，初中数学教学教师在几何证明题教学中，应多培养、多锻炼学生的逆向思维，从而提升学生的思维能力。
三、在应用题解题教学中的应用
应用题的综合性更强，对学生思维能力和逻辑推理能力的要求比较高。在应用题中若要采用逆向思维方法进行解题，就是要从问题入手，依次推理，直至找到所求结果与已知条件的关联。而后，再反过来一步步书写解题步骤，即可完成解题。但是逆向思维能力的培养并不是一件简单的事，需要长期的锻炼。为此，在初中数学解题教学中，教师要坚持引导学生应用逆向思维解题。长此以往，逆向思维意识便会深深地根植在学生脑海中。
例如：小红买了几瓶饮料，第一天，小红喝了全部饮料的一半和半瓶。第二天，做客的小明喝掉了第一天剩下饮料的一半和半瓶。第三天，小红又把第二天剩下饮料的一半和半瓶喝了。最终将饮料全部喝完。那么小红共买了多少瓶饮料。仔细分析题目能够发现，如果我们按照题干顺序解题，那么计算量会比较大。所以，我们可尝试从问题入手。假设经过第一天、第二天的消耗，还剩下x瓶水。则第三天小红喝的饮料瓶数为x/2-1/2=0，也就是x=1。那么假设经过第一天的消耗，还剩下y瓶水。那么小红第二天共喝的饮料瓶数为y/2-1/2=1，也就是y=3。那么继续假设在未饮料前，共z瓶水，那么小红第一天共喝的饮料瓶数为z/2-1/2=3，也就是z=7。那么小红就是共买了7瓶饮料。显然，采用逆向思维，反向解题更能简化解题难度。为此，在应用题的解题教学中，初中数学教师应鼓励学生大胆尝试应用逆向思维方式解决难题。不仅如此，初中数学教师还应当认识到逆向思维在应用题中的应用不仅仅限于这一种类型。但授之以鱼不如授之以渔，教师不仅仅要让学生拥有逆向思维思想，更要让学生熟练掌握逆向思维应用技巧。这样才能保证学以致用，避免生搬硬套。
综上所述，解题教学是初中数学教学的重要组成部分。为了真正提升学生的逆向思维解题能力，初中数学教师应在解题教学中，不断渗透逆向思维，并结合实例展示出逆向思维的应用方法。
参考文献：
[1]白北平. 逆向思维在初中数学解题教学中的应用[J]. 中学数学,2018(24):85-86.
[2]罗进. 例谈逆向思维在数学解题中的应用[J]. 中学数学教学参考,2016(12):39.
[3]方海文,李东,李春玲,康兆敏,毕秀芝. 数学教学中逆向思维训练探析[J]. 科技创新导报,2015,12(20):105+107.
论文作者:景银海
论文发表刊物:《未来教育家》2018年第12期
论文发表时间:2019/1/15
标签：思维论文; 学生论文; 应用题论文; 小红论文; 教学中论文; 抛物线论文; 顶点论文; 《未来教育家》2018年第12期论文;