吕晓薇 (上海市大众工业学校 上海 201800)
【摘 要】 数学是"三校生"高考的重要学科,而对于职业学校的学生而言,由于基础差,数学思维不强,解题方法单一,导致成绩不理想。因此作为授课教师通过其教学来提高学生解题能力便显得尤为重要。本文通过对三校生高考典型题的分析,阐述了培养三校生解题能力的重要意义。
【关键词】能力 数形结合 思维转换
中图分类号: G71 文献标识码: A文章编号:ISSN1004-1621(2014)02-064-02
一、引言
2014年2月26日国务院常务会议部署加快发展现代化职业教育,指出要全面提升人才培养模式,建立学分积累和转换制度,打通从中职、专科、本科到研究生的上升通道。三校生高考经过多年的实践,无疑是实现和通往中职向更高学历层次发展的一条重要途径。但是中职阶段的教育面临着生源质量差、学制短、重技术、轻文化等困境。同时,三门高考科目当中的数学是一门逻辑性强,培养学生思维能力的重要学科,需要学生有较强的分析和解题的能力。但是对于三校生而言,这门课程的学习却显得相当困难。其一:职业学校的课程设置中,技能学习占据总学时的50%左右,再加上以专业课占主导的理论课教学,数学课时的安排量便可想而知。其二:三校生基本上都是所谓的学习困难学生,初中阶段打下的基础比较薄弱,知识掌握不灵活,解题思路单一。其三:没有掌握有效的学习方法,课堂听讲效率较低,对于老师传授的知识只会死记硬背,依葫芦画瓢,需要掌握的公式只能机械背诵,一旦应用到解题上便不知从何入手,自身分析问题的能力相当有限。学习能力的欠缺直接导致学习兴趣不高,成绩得不到进一步提升。
面对这样的现实,如何破解数学在三校生高考中的这个难题,是中职校数学教师需要细心研究的一项重要课题。数学知识的灵活性要求学生锻炼出发散的思维能力,形成和构建一定的思维模式,以拓展自己的解题思路和方法。通过研究考纲不难发现,高考题的难易比率为基础题占40%,中等题占40%,较难题占20%。这项数据说明对于三校生来说,抓基础、重技巧是更好完成学习的关键。从教的几年中,本人逐步摸索出一定的教学规律:首先,对于基础题的掌握,要求学生熟记公式,能做到随问随答,为简单解题打好基础。其次,对于固定套路的题型,通过大量习题的练习让学生做到见题知方法,熟能生巧。最后,对于灵活多变的题型,在课堂上要能对条件进行透彻分析,通过解题指引、培养学生独立寻找解题思路,搭建解题构架,最终达到学习能力的提升。以下通过几道例题说明解题方法灵活运用的重要性。
二、剖析已知条件,题点逻辑化
在三校生高考的题型中,数列问题属于最贴近生活、灵活性也较强的问题。等差数列与等比数列的特性和证明是很容易被学生掌握的。在问题当中有很明显的条件提示时,较为容易发现方法并得到相应解决。但是当出现的条件灵活变化时,第一直觉无法观察出结论的时候,就无从下手,从而无法完成解题。
.jpg)
三、巧用数形结合,问题简单化
我国著名数学家华罗庚曾经这样形容数形结合:"数与形,本是相倚依,焉能分作两边飞。数缺形时少知觉,形缺数时难入微。数形结合百般好,隔离分家万事非。"这一首词形象地比喻了数形结合之间密不可分的关系。数形结合就是把抽象的数学语言、数量关系与直观的几何图形、位置关系结合起来,通过抽象思维与形象思维的相结合,将复杂问题简单化,抽象问题具体化,从而起到优化解题途径的目的。
例2:曲线C:x-y -2y=0上存在关于直线L:y=x+m对称两点A、B,求m的取值范围。
.jpg)
数形结合是高中学习的重要解题技巧,且学生已经得到很纯熟的训练,在某些题型出现的时候会自然想到这种方法。但对于中职生来说,知识积累量较少,而且方法掌握较死板,多数情况只会运用单一方法,而且纯代数方法有时增加解题难度,还会出现考虑不全面的情况。但是通过数形结合,会降低解题难度,所以在授课过程中应对很明显的与图形能相结合的题型多加练习,让学生在脑海中形成记忆,
四、 改变思维模式,方法灵活化
立体几何学习是一种空间思维想象能力的培养,它会帮助职业学校的学生更好的在今后的专业操作中解读零件图纸。同时在高考中也占有一定的分值。但是对于三校生来说,由于初中基础不扎实,平面几何内容掌握得不灵活,导致空间图形很难在脑海中形成图形框架。因此在教学过程中丰富教学情境、增加教学工具便成为重要环节。例如在线面平行、垂直的教学上要教会学生能够利用身边一切可以利用的小道具(笔或者书)构建小模型,形象的视觉呈现在面前的时候,知识便得以掌握。而对于高考常见的立体几何题型中,线面成角是典型考题。

类似于本题的题型,对于学生来说已经通过典型题的掌握可以直接找到顶点到底面的垂线,而常见题型垂线可以直接找到或者借助一条辅助线确定位置,进而利用垂线、射影、斜线构成的直角三角形三角比完成求解。但是对于垂线位置不确定的考题就会对学生造成很大困难。下面就这种类型的题目进行举例说明。
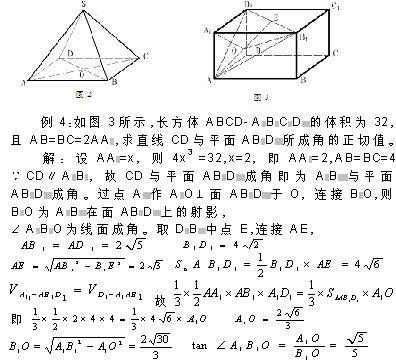
此题一出,在直观上造成了两大困难:首先,所给出的平面AB1D1是倾斜的,这对于学生而言视觉上产生了偏差;其次,根据分析会发现平移CD到A1B1后过点A1做出的垂线垂足位置无法确定,理由是该三棱锥不是正三棱锥,这样就给求垂线的长度制造了困难,所以转换求解垂线是关键的一步。对于三棱锥的特殊性,任意点都能作为三棱锥的顶点,而若以A1作为顶点,A1发出的三条棱两两相互垂直,明显能求出该三棱锥的体积。通过合理转换顶点,利用体积相同的原理,即使没办法确定高A1O的位置也能求出其长度,问题便迎刃而解。因此转换思维是解决立体几何当中很关键的一种方法,当常规做法遇到困难的时候,一定要利用条件转换的方法,因此教师在授课中遇到这样的题型一定要夯实,让学生能够对转换方法灵活掌握,从而使问题得以解决。
五、结束语
新东方创始人俞敏洪曾说过" 一个人要实现自己的梦想,最重要的是要具备以下两个条件:勇气和行动。"勇气"是三校生实现梦想的开始,而"行动"需要更明确、更有方向的指引。作为他们的指引者,我们更该在教育教学的道路上不断摸索、不断学习,让更多的学生能够在自己的人生道路上绽放光彩。
【参考文献】
[1]康小玲.数形结合法[J].四川:数学教学通讯,2002.
[1]张学军.中职"三校生"数学课高考指导如何教
[J].湖北:新课程研究,2012.
论文作者:吕晓薇
论文发表刊物:《科学教育前沿》2014年第2期供稿
论文发表时间:2014-4-18
标签:垂线论文; 题型论文; 学生论文; 三校生论文; 方法论文; 棱锥论文; 灵活论文; 《科学教育前沿》2014年第2期供稿论文;
