摘 要:初中阶段是学生学习基础知识的一个非常重要的阶段,该阶段学生学习的知识及形成的思维习惯会对其一生的学习能力造成很大程度的影响。数形结合思想是初中数学中比较重要的一种思维方式,它不仅可以有效培养学生的数学思维能力,而且还能迁移引用到物理等学科的学习中去。 本文浅析初中数学教学中数形结合思维的意义及主要表现形式,或可以抛砖引玉,促使数形结合这一古老数学思想在现代教育中绽放新的活力。
关键词:数形结合 教学思想 意义
一、数形结合在数学教学中的意义
数形结合是数学解题中常用的思想方法,用数形结合方法可以使复杂问题简单化、抽象问题具体化,能够变抽象的数学语言为直观的图形、抽象思维为形象思维,有助于把握数学问题的本质,有利于数学中两大研究对象“数”与“形”的矛盾统一。
在教学中渗透数形结合思想,有利于培养学生运用这种思想分析数学问题的意识。应用数形结合思想,可以不断增强学生分析及解决问题的能力。数形结合的思想有利于帮助学生建立普遍联系的思维方式,有利于寻找学科之间、章节之间的契合点,将数与行进行巧妙的结合,进而进行相互间的有效转化,能真正有效的解决相应的数学问题。
二、数形结合的主要表现形式
数形结合的思想内容一般表现为以下几个方面:一是代数建模(一般为方程、函数和不等式模型);二是几何建模(或者是函数图像),进而有效解决有关函数和方程的问题;三是同函数相关的几何、代数的综合性问题;四是利用图像形式呈现相应信息的应用问题。常见的表现形式有以下两种。
1.以数助形。要在解题中有效地实现“数形结合”,最好能够明确“数”与“形”常见的结合点,从“以数助形”角度来看,二者主要有以下两个结合点:
(1)利用数轴、坐标系把几何问题代数化(在高中还将学到用“向量”把几何问题代数化)。
(2)利用面积、距离、角度等几何量来解决几何问题,例如,利用勾股定理证明直角、利用三角函数研究角的大小、利用线段比例证明相似等。
例题:如图,在正△ABC的三边AB、BC、CA上分别有点D、E、F。若DE⊥BC,EF⊥AC,FD⊥AB同时成立,求点D在AB上的位置。
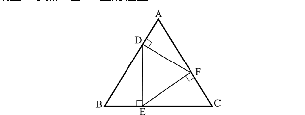
分析:从图形直观来看,D在三角形AB边上距离A点三分之一处。
从集合逻辑关系证明:
∵B=60°,DE⊥BC,在Rt△BDE中
∴BE= BD,∠BDE=30°
同理AD=AF,CF=CE,∠CEF=∠DFA=30°
∴∠EDF=∠DFE=∠FED=60°
∴△EDF为等边三角形,则ED=EF=DE
∴△BED≌△CFE≌△ADE
∴BD=AF=CE
∴AD=AF=BD
即D点在AB边上距离A点三分之一处。
2.以形解数。几何图形在数学中所具有的最大的优势就是直观易懂,所以在运用“数形结合”思想解决问题时,就更偏好于“以形解数”的方法,利用几何图形解决相关不易求解的代数问题。几何图形直观的运用于代数中主要体现在以下几个方面:
(1)利用相关的几何图形帮助记忆代数公式,如完全平方公式与平方差公式。
(2)利用数轴及平面直角坐标系将一些代数表达式赋予几何意义,通过构造几何图形,进而帮助求解相关的代数问题,或者简化相关的代数运算。
例题:已知如下图,P是正方形ABCD的边BC上的点,且BP=3PC,Q
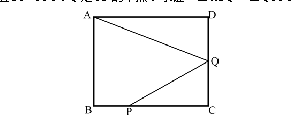
分析:∵四边形ABCD是正方形,且BP=3PC,Q是CD中点,若我们设正方形ABCD边长为4,则即可得到BP、PC、DQ、QC的具体值,最后可通过相似三角形各对应两两之比的比值相等这一性质得出△ADQ∽△QCP。
通过以上例题我们不难看出,在解决数学问题的时候如果能够有效的应用数形结合的思想,就会将一些十分复杂的数学题变得十分简单,从而获得比较清晰的解题思路,而且步骤明了。
数学是一项基础学科,在培养学生的理性思维能力、学习能力和解决生活实际问题的能力方面意义深远。数形结合的教学思想不仅可以有效培养学生普遍联系、综合解决问题的思维,还能促进学生分析数学问题和解决数学问题的能力,所以建议数学教师在这方面多思考、多探索、多运用。
论文作者:景满良
论文发表刊物:《教育学文摘》2015年9月总第168期供稿
论文发表时间:2015/9/25
标签:代数论文; 思想论文; 数学论文; 几何图形论文; 几何论文; 意义论文; 函数论文; 《教育学文摘》2015年9月总第168期供稿论文;
