摘要:自锚式悬索桥的成桥线形和空缆线形是其计算的关键部分,本文基于分段悬链线理论,采用有限元与解析算法相结合的思想,以压缩刚度的概念近似考虑成桥状态下主缆、主塔和主梁之间的相互作用,并根据施工各阶段无应力长度不变的原理,综合考虑桥塔处鞍座预偏量、压缩变形等因素的影响,从成桥状态倒拆出空缆状态主缆的线形。
关键词:自锚式;悬索桥;主缆线形;计算方法
引言
随着国民经济和交通事业的快速发展,人们审美需求的不断提高,桥梁的跨越能力和靓丽外观逐渐占据重要地位,自锚式悬索桥因其造型新颖、跨越能力强、对地质条件要求低等特点,现已成为中小跨径桥梁中具有较强竞争力的一种桥型,尤其是在软土地区和城市景观桥梁中,自锚式悬索桥越来越受到青睐。
自锚式悬索桥的主缆直接锚固在主梁上,在成桥状态强大的水平张力和竖向力的作用下,势必会造成主梁、主塔的压缩,从而影响主缆线形,精确计算自锚式悬索桥的成桥线形与施工过程中的变化特性已成为该类桥梁设计与施工控制的关键技术问题,而主缆线形又是成桥线形的决定因素之一。
1、主缆成桥线形计算方法
缆索线形的计算通常作以下假设:①索是理想柔性的,只能承受拉力,而不能承受压力和弯矩;②索材料处于弹性阶段工作,满足虎克定律,同时索的应变满足小应变的假定;③忽略主缆的截面面积和自重在荷载作用下的变化量。
成桥状态下自锚式悬索桥主缆的受力可近似看作沿弧长承受自重下均匀荷载和在吊杆上吊点处承受集中荷载(包括加劲梁等效质量、吊杆、索夹和二期铺装等)。吊点与吊点间的主缆可视为只受主缆自重的悬链线,即整个主缆可以按吊杆的上吊点划分为多段悬链线的组合,吊点处的集中力作用在每段悬链线两端的位置。
根据上述3个假设及主缆受力的论述,各段缆索均需满足式(1)和式(2)。
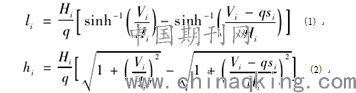
式中:q为主缆自重荷载;Hi表示第i号索段两端的水平力;Vi表示第i号吊索的竖向力;si为第i号索段间的有应力索长;li为第i号索段间两吊点之间的水平距离;hi为第i号索段两吊点间的高差。
在主缆成桥线形计算时,加劲梁的质量、主缆的自重荷载q、主缆各吊点之间的水平距离li、跨中矢高f、鞍座两侧悬链线的顺延线交点的坐标以及主缆锚固点均是已知的,并假定整个求解过程中主缆变形已完成,即认为是有应力索长参与运算。索段的无应力长度可通过成桥状态有应力索长反算求解,即无应力索长等于有应力索长si减去第i号索段的弹性变形量Δsi,同时应考虑架设温度的影响对无应力长度进行修正。式(1)、式(2)是一组非线性方程组,可以通过确定内力与线形误差之间的关系进行迭代求解。当一个跨内所有索段完成计算后,由于成桥状态鞍座位置已固定,成桥状态下鞍座处不会有位移发生,在进行其他相邻跨内索段分析时,可假设各鞍座处主缆水平力相等。
以上成桥主缆线形的计算过程可编制解析程序求解,通过输入计算所需的设计参数,得到成桥状态下主缆索力的水平分量、竖向分量、每个索段主缆的吊点坐标及每个索段的无应力索长。
2、主缆空缆线形计算方法
大量研究表明,当悬索桥各索段的无应力长度及作用其上的荷载确定后,结构最终的约束条件也是确定的,那么其最终状态也是唯一确定的。反之,只要悬索桥的最终成桥状态的主缆线形和结构内力确定,其空缆线形也是唯一确定的。所以,空缆线形的计算以成桥状态迭代计算的无应力长度为基础,通过满足锚固端、桥塔及鞍座处实际的平衡条件,完成各索段的循环分析。
2.1、索鞍处预偏量的计算
在空缆状态下主缆上只有缆索本身自重作用,此时还未受到梁段、索夹、吊索等外荷载作用,与成桥状态相比主缆内力将会减少,同时主跨荷载减小得多,边跨荷载减小得少,如果索鞍仍保持在成桥状态的位置,势必会在索鞍处产生强大的不平衡力,造成桥塔偏位、成桥时线形无法达到设计标准,因此需要在鞍座处进行预偏量设置,保证架缆时桥塔不偏位、鞍座内主缆索股不滑动,以至吊杆张拉过程中通过鞍座顶推,使得成桥状态体系转换后可以达到预期设计要求的成桥线形。
预偏量的设置需要满足以下条件:①鞍座两侧主缆沿鞍座滑移面的水平分力相等;②空缆状态下各索段间无应力长度与成桥时相等。因此,鞍座偏移量的计算可由鞍座处主缆支撑点的滑移刚度以及桥塔的抗弯刚度,根据力和位移的关系确定。
2.2、主梁、主塔处压缩刚度计算
对于自锚式悬索桥而言,由于缆索系统直接锚固在主梁上,使得主梁、主塔承受缆索传来压力作用,这将使其产生一定的压缩变形。在空缆状态下,由于主缆索力较小,主梁、主塔刚度较大,因此压缩变形较小,可以近似忽略;在成桥状态下,由于主缆受到主梁、吊索的作用,使得主缆产生较大的索力,如果仍按照设计位置进行空缆架设,当成桥状态施工完成后,主梁、桥塔部位势必会因压缩变形的影响,无法达到成桥时的设计线形、内力等要求。因此,在空缆架设时,应以主梁、桥塔的设计位置加上压缩变形后得到的实际锚点位置作为架设基点,使得整个悬索桥建设完成后能满足设计要求。
2.3、空缆线形计算流程
空缆线形的计算是以成桥状态为基础倒推出整个空缆状态下主缆线形。根据无应力长度不变原理和主缆的质量守恒,以成桥状态计算出的无应力长度、各个索鞍的初始位置和截面特性等作为初始条件,通过塔-梁有限元模型预估出初始压缩变形,以压缩刚度的形式近似考虑主梁、主缆以及主塔共同工作的影响,迭代求解出最终的压缩变形,根据变形值计算出空缆状态下实际的锚固点坐标,然后通过抛物线理论计算出一端主缆的初始水平力和竖向力,采用与成桥线形计算相同的思想,通过悬链线方程进行各跨内每个索段的循环,判断另一端点的坐标是否与控制点坐标相符,如相符就说明假定的索端水平力、竖向力值正确,否则需要通过影响矩阵法修正假定值重新计算,直到满足收敛精度。
在悬索桥的鞍座和每个锚固跨散索鞍处需要进行预偏量的计算,首先假定各鞍座的初始偏移量,根据每个索段的主缆无应力长度,计算其空缆线形及鞍座处缆索力,检验各个鞍座处两侧的力和位移是否满足平衡条件,若满足说明假定值就是真实值,否则就得重新进行各个跨内线形的计算,直到满足平衡条件为止,输出满足平衡条件修正后空缆状态下各跨吊点的坐标。
总而言之,自锚式悬索桥结构新颖、外形美观,近年来在城市桥梁中应用较为普遍。主缆是自锚式悬索桥的主要承重结构,悬索桥的结构线形主要受主缆线形的控制。
参考文献
[1]丁松.空间索面悬索桥主缆线形分析及程序开发[D].燕山大学,2016.
[2]李鹏昊.自锚式悬索桥受力特性研究[D].浙江大学,2016.
[3]谢小龙.独塔空间索面自锚式悬索桥施工关键技术研究[D].重庆交通大学,2016.
[4]杨鑫.三跨空间索面自锚式悬索桥施工关键技术研究[D].重庆交通大学,2016.
[5]严琨,沈锐利.基于细长梁单元的悬索桥主缆线形分析[J].计算力学学报,2016,03:381-387.
论文作者:李春辉
论文发表刊物:《基层建设》2017年第24期
论文发表时间:2017/11/13
标签:悬索桥论文; 缆线论文; 线形论文; 应力论文; 缆索论文; 荷载论文; 状态论文; 《基层建设》2017年第24期论文;
