关键词：水击；数值模拟；关闭规律
1 前言
水击现象是城市输水管道系统设计和运行管理考虑的重要因素之一。阀门的突然启闭产生的巨大压力可能导致管道的剧烈振动甚至爆炸，造 成严重事故，给社会和人民带来巨大的经济损失。因此，研究计算水击压力，探讨水击波在管道中的传播规律，研究防止和削弱水击作用的 技术措施，减少水击带来的经济损失，对城市供给管道的建设、运行和管理有着重要的技术经济意义。
TVD格式是一种高分辨率激波捕捉方法，在激波间断附近不会产生非物理振荡，目前已在空气动力学和溃坝水力学等领域得到了成功而广泛 的应用[1-3]。水击波也是一种激波，刘韩生等[4-6]成功应用TVD格式数值模拟水击得到了良好的效果。本文采用Harten构造的经典TVD格式 研究分析市政管道系统阀门关闭时间和关闭方式对水击压强的影响，证实TVD格式是数值计算水击行之有效的方法。
2 水击的控制方程
考虑水头损失和管道倾斜的影响，一维水击的控制方程是一组拟线性双曲型偏微分方程，可以描述为[7]：
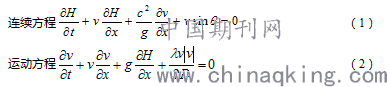式中：H为测压管水头；v为管道断面流速；c为水击波速；D为管道直径； 为管道倾斜度； 为沿程水头损失系数。
3数值模拟计算
TVD格式是一类比较成功的激波计算方法，只要采用统一的计算格式，便可自动求得激波的位置、强度和运动，具有分辨率高，激波间断处 不产生非物理振荡等优点[4]。自1983年Harten[8]提出以来，国内外很多学者在他研究的基础上继续研究并构造了其他高精度无波动格式得 到了广泛的应用。本文采用经典的Harten构造的修正通量TVD格式进行水击计算。
将水击控制方程组写成守恒形式为[4]：
5算例
某城市供水管网工程有一水平放置的管径不变的供水钢管，进口与水库相连，末端为阀门。已知管长L=500m，管径D=1m，恒定流时管中流速 v0=4m/s，静水头H0=100m，管壁厚度 =10mm。管壁粗糙系数n=0.013。将阀门快速关闭，管道中将产生水击现象。本文采用前文介绍的TVD格 式计算阀门规律对水击压强产生的影响。
阀门关闭时间
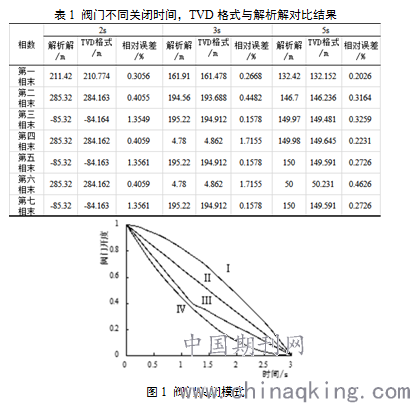
表1反映的是不考虑水头损失时，阀门按直线规律关闭，关闭时间分别为2s、3s、5s时，阀门末端不同相末水击压力大小。随着阀门关闭时 间的延长，阀门末端水击压力随之减小。通过对比解析解，说明TVD格式具有相当高的计算精度，最大相对误差不超过2%，能够有效的计算 管道水击压力大小。
（2）阀门关闭方式
固定阀门关闭时间Ts=3s，通过改变阀门关闭速度，按图1所示的阀门关闭方式进行计算。模式Ⅰ、Ⅳ按曲线关闭规律，模式Ⅱ直线关闭规律 ，模式Ⅲ两阶段直线关闭规律由全开至完全关闭。从图2中可以看出，阀门关闭时间一定时，不同的关闭方式对管道产生的最大水击压强有 较大的影响。模式Ⅰ和Ⅳ虽然都是按曲线方式关闭，但前者关闭速度先慢后快，后者相反，结果有较大的反差。模式Ⅰ产生的水击压力最大 ，且管道中出现负水击，管道水击振荡强烈；模式Ⅳ产生的水击压力变化先快后慢，振荡较小，最大水击压强相对较小；模式Ⅱ和Ⅲ都是按 直线规律关闭，相比较而言，两阶段关闭方式产生的水击压力明显小于其他关闭方式，且6s以后水击压力趋于平缓。
表1 阀门不同关闭时间，TVD格式与解析解对比结果
5 结论
本文采用经典TVD格式对有压管道阀门不同关闭规律的条件下产生的水击现象进行了数值模拟。通过改变阀门关闭时间以及关闭方式，计算 阀门末端水击压力的变化过程。计算结果表明：TVD格式具有较高的计算精度，能够有效地数值计算管道水击压力。阀门直线关闭规律条件 下，关阀时间越快产生的水击压力越大；关闭时间一定时，阀门关闭方式对管道水击压力变化的影响不同，直线关闭产生的压力大于两阶段 关闭，采用曲线规律加速关闭产生的水击压力大于减速关闭。因此工程上应尽量采用两阶段关闭或减速关阀的方式减小最大水击压力。
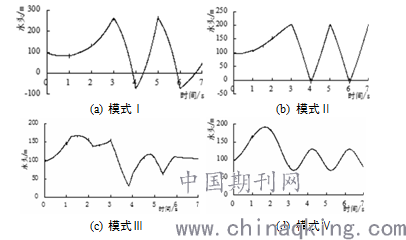图2 不同关闭模式阀门末端压力水头变化过程线
参考文献
[1].谢禁睿，吴颂平.TVD格式与高超音速气动加热数值模拟[J].北京航空航天大学学报，2007,33（4）：392-396.
[2].袁湘江，桂业伟，涂国华等.捕捉间断的高精度数值方法[J].空气动力学学报，2004,22（3）：269-273.
[3].王嘉松，倪汉根，金生等.用TVD显隐格式模拟溃坝波的演进与反射[J].水利学报，1998，（5）：7-15.
[4].刘韩生，樊书刚，张丹，张一.TVD格式在水击数值模拟中的应用[J].水力发电学报，2010，（4）：107-112.
[5].张丹，刘韩生，李顺兵等.水击的数值模拟方法比较[J].人民长江，2008，（18）：75-76.
[6].黄逸军，刘韩生.TVD格式在上游调压室水击数值模拟中的应用[J].长江科学院院报，2013,30（5）：47-50.
[7].E.B怀利，V.L.斯特里斯.瞬变流[M]。清华大学流体传动与控制教研组译.北京：水利水电出版社，1983.
[8].Harten A.High resolution schemes for hyperbolic conservation laws[J].J.of Comp Phy.1983,49: 357- 393
论文作者:董瑜
论文发表刊物:《基层建设》2018年第20期
论文发表时间:2018/9/17
标签：阀门论文; 压力论文; 管道论文; 格式论文; 数值论文; 规律论文; 方式论文; 《基层建设》2018年第20期论文;