湖南省株洲市茶陵县腰陂中学 邮编：413200
摘要:本文运用构造一元二次方程的方法求解一类相关的竞赛题，通过列举一些例子如：循环式求值、解高次方程、求代数式的值，求范围、证明几何问题等进行分析解答，渗透重要的数学思想—化归思想，同时对如何运用基本知识解决较难问题在转化策略上进行详细的阐述，这对同步训练培优辅导都能起到较好的引领作用。构造法形式很多，变形巧妙独特，引人入胜。
关键词：构造法、一元二次方程、根与系数的关系、主元、化归、
构造法是数学解题方法中的一个瑰宝，构造的形式很多，如构造函数、方程、不等式、数列及图形等，这种方法的运用是需要有较强的观察、分析和思维能力，因而在较难求解的数学问题上尤其是竞赛中运用的比较多。下面就初中数学解题中运用构造一元二次方程求解问题谈点技巧上的做法。有些数学问题，表面上看起来很难解，似乎与一元二次方程求解没有关系，但若变换角度思考，善于发掘出其特征，利用一元二次方程来处理，则能达到事半功倍之效。
一、化无限为有限，构造一元二次方程求值
有些需要化简求值的式子，尤其是无限嵌入循环式，非常不便变形化简，我们可以通过构造方程来求，容易达到目的。
例1、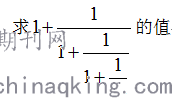
解析：这类问题是一个无限循环式，直接去计算，可以说寸步难行，利用数学中的化归思想，将“无限”变“有限”处理，方能找到解决的途径。而实现这种转变，必须通过构造法来完成。设所求式
二、反客为主，利用根的定义构造一元二次方程
1、含参数的高次方程求解
有些高次方程，直接求解是十分困难的，这时可以对方程重新定位，变换角色，让“未知”变“已知”，即变“客”为“主”，这样就取得解决问题的主动权，从而化归到熟悉领域进行处理，较快地解决问题。
2、求有条件的代数式的值
这类问题中若给出的条件是等式，直接利用所给条件又很难时，可以考虑条件特征，通过构造方程将条件进行变换求解。
三、选择主元构造一元二次方程
对含有多个未知数的等式，选择其中一个未知数作为主元，整理成一元二次方程的一般形式，就可将问题转化为解一元二次方程来处理。
四、逆用根与系数的关系构造一元二次方程
当遇到有些问题中的条件有或能转化为 
形式时，可以反用根与系数的关系实现构造一元二次方程，从而使问题迅速求解。
.png)
论文作者:孟宪南
论文发表刊物:《未来教育家》2019年07期
论文发表时间:2019/8/6
标签：方程论文; 条件论文; 代数式论文; 形式论文; 系数论文; 数学论文; 关系论文; 《未来教育家》2019年07期论文;