西北工业大学启迪中学 钱迎博
摘要:随着新课改的不断深入,在初中数学教学中不断应用新的教学方法,旨在提升学生的思维能力和创新意识,而建模思想应用于初中数学教学中对学生观察能力、思考能力和数形结合能力的提升有重要的促进作用,进而提升学生数学核心素养。基于此,本文以“相似三角形的应用”为例,分析如何利用建模思想开展数学教学,希望具有借鉴意义。
关键词:初三数学;建模思想;相似三角形;实际应用
在数学课程标中要求,学生要在理解数量关系以及变化规律的前提下,从实际问题中具备构建数学模型的能力,可以进行估计、求解和验证。因此,数学建模使初中数学学习的重要手段,有利于学生界回族该手段解决实际问题。作为一名初中数学教师,要合理利用该方法使学生体会建模思想与生活的密切关联,培养学生的数学核心素养。本文以北师大版教材九年级数学上册《相似三角形的应用》为例,做出详细说明。
一、教学目标
(一)知识与能力目标
教师需要在教学中让学生发现生活中常见的相似三角形模型,同时还要培养学生的观察和分析能力,可以根据不同的情境构建出形似的模式,去解决在不具备测量长度的情况下利用建模解决实际问题的能力。此外,教师还要培养学生数形结合的能力,可以从不同的角度思考问题,并且表述解答过程。
(二)过程与方法
在确定教学目标的前提下,教师要精心设计教学环节,在利用建模思想教学时,教师要注意兴趣的引导,通过有效的交流和典型题目使学生深入思考。同时,教师为学生提供数学例题,引导学生把实际问题转化成相似三角形的数学模型,进一步使学生了解建模思想,强化分析问题的能力以及应用能力[1]。
(三)情感、态度和价值观
教师要为学生提供问题情境,引发学生主动思考和动手操作,让学生寻找相似三角形的形成以及问题如何解决。同时,教师要注意学生自信心的培养,而利用建模思想开展教学可以有效提升学生的学习动力。常言道:“兴趣是最好的老师”。教师要利用建模思想引导学生在问题的解决中体会学习的快乐。
二、教学过程
(一)创设情境,体验数学建模
例题:周末下午,阿雷和爸正在公园散步,阳光照在两个人身上留下影子,阿雷的身高为1.5m,影子长1.2m,而爸爸的影子长1.44m,问如何求出爸爸的身高。对于这道题来说,学生就可以利用建模思想求解,教师需要做好板书,同时学生通过搭建模型并展示成果,然后教师提出问题:“借助建模思想同一时间知道阿雷的身高和影子长度应该如何求出爸爸的真实身高?”引导学生口头回答,而教师展示板书的内容也正是甲物高/甲物影长=乙物高/乙物影长,学生利用建模思想可以得到1.5/1.2=X/1.44,教师把生活问题与数学问题结合起来,引导学生利用几何知识解答,这样更加容易被学生接受,从简单的问题探索规律,找到解决问题的常规步骤,进而提升学生的数学能力[2]。
(二)把握策略,渗透建模思想
测高是常见的相似三角形模型,教师可以继续举例。西安大雁塔高54.5米,但是如果教师只给学生2米的木杆和一把米尺,学生可以测出塔高度吗?其实结合建模思想可以利用图一表示出来。
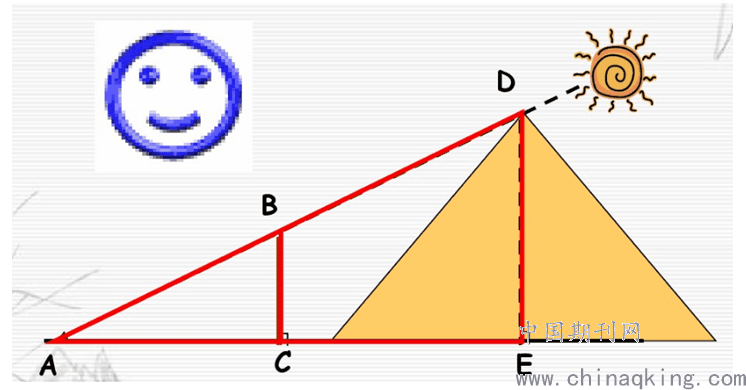
图一
这道数学题同样用到了相似三角形的内容,在解答中需要学生在图上标注数字进而解答,分析:由于∠DAE=∠BAC,且BC平行DE,所以三角形BAC与三角形DAE形似,通过相似三角形相关知识可知,建模思想是用数学方法解决实际问题的过程,每一个数学问题都没有固定的解答策略,而该道题恰好培养了学生数形结合的思想。接下来教师继续为学生出题:阿雷利用米尺BE测量教学楼的高度,如果直尺BE长度为120cm,同时AB =160cm,BC =124cm,问楼高CD为多少cm?(如图二)
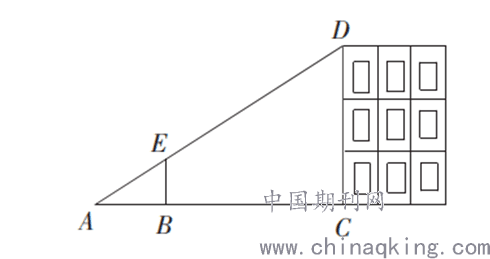
图二
由于之前已经在例题一中向学生渗透建模思想,因此教师可以让学生自行设计测量方案,然后归纳相似模型。教师在利用建模思想教学时,要对给学生提供思考和实践的机会,培养学生制定测量方案,提炼相似模型,进而强化建模能力。
(三)课堂小结
教师利用建模→解题→还原实际问题的方法方法开展教学,学生经过趣味性教学内容的学习,已经具备较好的问题解答能力,教师可以继续向学生提问:“大家还见过哪些常见的相似三角形模型”?学生就会说出交通灯投影,大树投影等内容,这样学生就会深刻体会到建模思想与生活的密切关系,同时学生数形结合的能力得到了培养。通过本节课的学习,学生的实践能力得到极大的培养,并且产生浓厚的学习兴趣,凸显了学生的主体地位[3]。
结语:综上所述,在素质教育背景下,广大初中数学教学正在利用数学建模思想开展教学活动,尤其是在初中几何教学中,该方法可以有效提升学习效率。因此,在今后的数学教学中,教师要多为学生提供数学建模的机会,侧重培养学生的思考意识,使学生形成良好的思维能力,促进学生数学核心素养的养成,进而为高中的数学学习打下基础。
参考文献
[1]初中数学教学中建模思想的应用探讨——以“相似三角形的应用”为例
[2]邵希军. 建模思想在初中数学中的应用——以鲁教版的教材为例[J]. 才智, 2016(2).
[3]彭慧秀. 基于几何直观的初中数学教学实践研究——以全等三角形和相似三角形为例[J]. 新课程(中), 2015(11):130-131.
论文作者:钱迎博
论文发表刊物:《现代中小学教育》2019第2期
论文发表时间:2019/4/8
标签:建模论文; 角形论文; 学生论文; 思想论文; 教师论文; 数学论文; 能力论文; 《现代中小学教育》2019第2期论文;
