摘要：随着高铁的快速发展，使人们的出行变得更加的便利，由于它舒适、快速的优势，高铁在远距离出行方面有无法代替的优势，为人们远行节约了很多时间。
首先，我们对数据进行预处理，根据各个城市不同的经济发展水平得出不同城市高铁配置的最佳数量，使得高铁可以发挥最大功效，最大程度上减轻高速公路的运行压力，公司利益最高，也使得旅客更加方便的出行。通过Excel对其做数值统计处理，然后将处理后的数据用Matlab软件中的相关函数对其进行计算，结合Excel、Maple优化软件与Matlab软件画图分析，最终对相关的问题做出结论。
关键词：高铁；高速公路；线性规划；最优配置
1、问题背景
随着人们生活质量的不断提高，几乎每家都拥有了私家车，从而造成高速公路拥堵的情况时而发生。但是随着中国高铁的迅速发展，给人们的出行带来了极大的便利，高铁的修建一方面能够缓解普通列车的运行压力，另一方面对高速公路的运行也起到了减压的作用。
2、问题重述
高铁即快捷，又舒适，但是相对于普通列车出行价格相对昂贵，因此不同地域的人出行方式的选择将会有所差异，请你选择发展不同的城市，尝试给出你所选城市高铁配置的最佳数量。
3、问题分析
通过对问题的分析，对城市高铁配置的最佳数量问题，我们考虑了三组相关因素。对因素一，通过对数据的搜集与整理，得到了影响旅客出行方式选择的各个因素，进而建立了旅客出行方式选择模型。通过对变量的量化，在出行者特征、运输方式特征两方面进行了相关的建模与分析。对因素二和三，运用优化模型对高铁的配置数量问题进行了优化分析，然后运用线性规划，利用Matlab进行求解。
4、模型假设
（1）假设数据经过微处理后对结果的影响并不大；
（2）假设收集整理的数据可靠真实；
（3）数据中的奇异数据在忽略后对总体结果没有显著的影响；
5.模型的建立与求解
5.1相关因素
对城市高铁配置的最佳数量问题，我们考虑三组相关的因素：乘客出行方式的选择、高铁、高铁站
5.2高铁最优配置的分析与建模
高铁达到最优配置问题，所求的方案既要考虑高铁公司的利益也要兼顾乘客自身利益。但在实际问题的分析上，双方不可能同时达到最优值。因此本文将高铁公司的利益作为主要目标函数，乘客利益作为其约束的条件。[1]
公司利益：
其中S为总收入，在这看作定值，为支出。
.png)
分析原目标值Z，易知.png)
。在以下分析计算中，以1小时为一个时间段来进行求解计算。
参数b：表示超过20分钟的候车人数占总候车人数的比重。当满载率大于或等于50%时，由于目标值为maxZ，则可以忽略不考虑，因此可得到如下模型：
.png)
通过分析可以发现：
i）对于上行车道，上车人数>下车人数；
ii）对于下行车道，上车人数>下车人数；
因而对于乘客利益这一约束条件，只需要取前4个值，对于此模型，通过拟合函数和将其约束条件转化为关于T的函数，然后再利用Matlab软件进行相应的求解。[2]
分析所得结果，在高峰时间段中，所得结果有较大误差，通过分析可知这是拟合函数的误差而引起的。为减小这一误差，假设在每小时内，到达每站的人数与时间成正比，在每站下车的人数也是与时间成正比的，即.png)
，于是将模型简化为：
.png)
当上行时，取所有约束条件，下行时取前5个约束条件。由于该模型为线性规划模型，因此可以利用Matlab进行相应的求解。
5.3高铁公司调度模型的建立
通过相关的计算分析，建立了一个线性规划模型，用Maple优化软件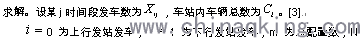
为总班次
.png)
若考虑到各站点乘客上下车时间相等，每辆车载1100人。在初步解的模型中，用Maple软件包优化选择，j=2，3…18。计算出整体最优解为：=62 =4，m=66，Z=476。
5.4部分城市高铁配置的最佳数量
通过对高铁配置模型的建立与求解，在此求出了北京、上海、广州、深圳、青岛、济南、哈尔滨的高铁配置的最佳数量。
.png)
参考文献：
[1]傅昌建，《关于公交车调度的优化问题》，《工程数学学报》，2002-12-30
[2]刘玥，《高铁数据与回归分析拟合上海和郑州高铁最优数量研究》，《数字技术与应用》，2019-04-26
[3]文生平，《基于市场分担率的高速公路客运区域竞争力研究》，西南交通大学，2015-05-01
作者简介：
阮帅（1999—），男，汉族，江西省九江市，学校：江西理工大学应用科学学院，专业：冶金工程；
李龙飞（2000—），男，汉族，四川省南充市，学校：西华大学，专业：数学与应用数学。
论文作者:阮帅1,李龙飞2
论文发表刊物:《基层建设》2019年第32期
论文发表时间:2020/4/8
标签：高铁论文; 模型论文; 线性规划论文; 数量论文; 人数论文; 最优论文; 数据论文; 《基层建设》2019年第32期论文;