摘要：基于正交异性板竖向荷载作用下的弯曲平衡微分方程式推导了开口加劲肋正交异性板的简化方程，采用横向分配杠杆法原理，推导了车辆轮载下单个加劲肋的荷载分配系数的计算公式，并编制算例将平面单梁法得到的结果和板壳有限法相比较，验证可靠性。
关键字：钢桥、桥面、正交异性板、第二体系
1.引言
由纵肋、横肋以及桥面盖板所组成的共同承受车轮荷载的钢桥面结构，由于其刚度在互相垂直的两个方向上有所不同，一般呈现出构造正交异性板。
钢盖板是纵横肋的上翼缘，正交异性板又是主梁的上翼缘，其共同受力，传统的分析方法是把它分成三个结构体系加以研究：
（1）体系I由盖板和纵肋组成主梁的上翼缘，与主梁一同构成主要承重构件—主梁体系。体系I分析的关键是确定翼板有效分布宽度，可以按照规范[3]进行计算。
（2）体系Ⅱ由纵肋、横梁和盖板组成的结构，盖板成为纵肋和横梁的共同上翼缘—桥面体系。目前规范[3]没有简化算法的规定。
（3）体系Ⅲ仅指盖板，它被视作支承在纵肋和横梁上的各向同性连续板—盖板体系。盖板应力可呈薄膜应力状态，盖板具有很大的超额承载力，所以在钢桥面静力计算中，结构体系Ⅲ的应力可以忽略不计[1]。
在荷载作用下，钢桥面板任意点的内力（或应力）可由上述三个基本体系的内力（或应力）经适当叠加而近似求出，钢桥面板体系Ⅱ的分析是难点。
目前体系Ⅱ的分析方法主要假定为支承在主梁上的正交异性板，常见的分析方法有P-E法、H.Homberg的格梁法和薄壳有限元法。P-E法通过编制相应的图表，可以通过手算求解桥面结构的内力，但是手算和查表工作量大。H.Homberg的格梁法将横肋和纵肋简化为支承于主梁和横梁腹板的梁格，需要手动建立桥面结构的梁格模型，过程较为复杂耗时。薄壳有限元法将桥面结构按照薄壳进行考虑，按照实际的几何尺寸建立模型，并且可以精确模拟车辆荷载的加载位置，但是这种方法无法将钢箱梁的三个体系应力分开求解。
本文提出一种平面单梁法，可以方便快速的求解开口加劲肋正交异性桥钢桥面板第二体系效应。
2.平面单梁法理论推导
2.1 开口加劲肋正交异性桥钢桥面板力学特性
正交异性板在竖向荷载作用下的弯曲平衡微分方程式为[2]：
.png)
（2-1）
钢桥面横向抗弯刚度Dy为桥面盖板的抗弯刚度。由于桥面纵向抗弯刚度Dx远大于Dy，由于Dx/Dy的比值通常为500～2000，故可认为Dy≈0，而开口纵肋加劲的正交异性板，其有效抗扭刚度H也很小，同样可假定H≈0。据此方程可以简化为：
.png)
（2-2）
.png)
图1 开口加劲肋正交异性桥钢桥面板力学示意图
假定车辆轮载在y方向分配系数为η，则q（x，y）=ηq（x），由此开口加劲肋正交异性桥面板体系Ⅱ求解问题就简化一维多跨连续梁的分析问题。
在桥梁设计中，针对多片梁的上部结构形式常通过求解荷载横向分布系数的方法，将桥梁空间问题简化为平面单梁问题，常用的荷载横向分布系数求解方法有杠杆法、偏心压力法、铰接梁法和刚接梁法，结合开口加劲肋正交异性钢桥面板的力学行为特点，车辆轮载在y方向的横向分配系数η，选用杠杆法进行计算。
2.2 轮载横向分配系数η推导
车辆轮载假定为横向假定为宽度为a’的均布荷载作用在钢桥面铺装层，均布荷载经过扩散为宽度为a的均布荷载，选取居中的纵向加劲肋为研究对象，加劲肋的间距为b，根据荷载分布宽度a和加劲肋的间距b的关系，存在两种不同的工况：
工况1：.png)
，轮载经桥面铺装层扩散后，荷载分布宽度a在杠杆法横向分布影响线范围之内，如图2所示：
.png)
图2 轮载横向分配系数η推导示意图（工况1）
根据力的传递原理可以得出，假设车辆轮载F，在桥面铺装层横向作用分布宽度为a’，荷载集度为q’；经过铺装层扩散后在钢桥面上的分布宽度为a，荷载集度为q，表示如下：
.png)
（2-3）
桥面铺装层的厚度为d，铺装层扩散后在钢桥面上的分布宽度a为：
.png)
（2-4）
根据影响线图乘法可以得出，单根加劲肋分项荷载R为：
.png)
（2-5）
所以轮载横向分配系数η为：
.png)
（2-6）
工况2：.png)
，轮载经桥面铺装层扩散后，荷载分布宽度a超出杠杆法横向分布影响线范围之外，如图3所示：
.png)
图3 轮载横向分配系数η推导示意图（工况2）
根据影响线图乘法可以得出，单根加劲肋分项荷载R为：
.png)
（2-7）
所以轮载横向分配系数η为：
.png)
（2-8）
综上可得：当 .png)
， .png)
；当 .png)
，.png)
。其中a为车辆轮载经过铺装层扩散后在钢桥面上的分布宽度，b为纵向加劲肋的横向宽度。
3.算例及验证
某城市匝道钢箱梁钢桥面主要参数如下表：
表1 钢箱梁钢桥面主要参数表（mm）
.png)
根据《城市桥梁设计规范》[4]，城-A级车辆荷载总重70t，立面和平面布置如图4所示
.png)
图4 城-A级车辆荷载布置图
3.1 平面单梁法
3.1.1 荷载横向分配系数
根据表1中的钢箱梁钢桥面参数和《城市桥梁设计规范》可以得：
加劲肋间距b为320mm，即 ，所以
单根纵向加劲肋车轮荷载分项系数
3.1.2 midas单梁分析
采用Midas梁单元建模，取6个隔板间距的纵向加劲肋进行桥面第二体系计算，模型如下
.png)
图5 Midas单梁模型图
3.1.3 单梁计算结果
.png)
图7 倒T肋上缘应力包络图（MPa）
由平面单梁法计算得倒T肋跨中最大拉应力为77.8MPa，支点最大拉应力为26.8MPa。
3.2 板壳有限元模型
为了验证平面单梁法计算的方法的准确性，建立了板壳有限元模型进行对比分析。
3.2.1 加载位置及有限元模型
根据前面midas单梁模型应力包络结果，选取倒T肋跨中最大拉应力（工况1）和支点最大拉应力（工况2）两种加载工况建立板壳有限元进行分析，利用移动荷载追踪器，找出两种工况下车辆轮载的布置形式，如图8、图9所示：
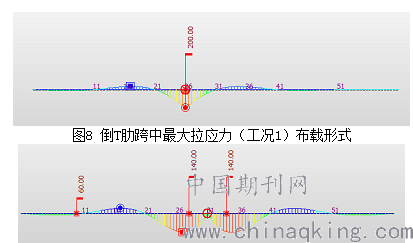
图9 倒T肋支点最大拉应力（工况2）布载形式
纵向选取6个节间钢箱梁，建立板壳有限模型，如图10所示：
.png)
图10板壳有限元模型
3.2.2 板壳有限元计算结构
.png)
图11 倒T肋跨中下缘最大拉应力（工况1）（MPa）
.png)
图12倒T肋支点上缘最大拉应力（工况2）（MPa）
由板壳有限元法分析得，倒T肋跨中最大拉应力为76.3MPa，支点最大拉应力为22.0 MPa。
3.3 计算结果汇总
表2 平面单梁法和板壳有限元结果对比表（Mpa）
.png)
根据表2汇总的结果可以看出，平面单梁法分析结果与板壳有限元法相比较，计算结果相近，证明了平面单梁法计算结果的准确性满足工程要求。
4.结论
（1）开口加劲肋正交异性桥钢桥面板第二体系效应可以通过引入荷载横向分布系数，可以简化为平面单梁分析。
（2）平面单梁分析法与板壳有限元模型两者分析结果相近，准确性满足工程要求。
参考文献：
[1]. 吴 冲 强士中 .现代钢桥[M] 北京：人民交通出版社.2011
[2]. 贺拴海.桥梁结构理论与计算方法 [M].北京：人民交通出版社 2003.
[3]. JTG D64-2015，公路钢结构桥梁设计规范[S]
[4]. CJJ11-2011，城市桥梁设计规范（2019版）[S]
作者简介：诸志强（1988-），男，工程师。2013年毕业于西南交通大学桥梁与隧道专业，工学硕士（zhuzhiqiang_brdi @163.com）。
论文作者:诸志强
论文发表刊物:《建筑模拟》2020年第2期
论文发表时间:2020/4/14
标签：荷载论文; 桥面论文; 正交论文; 横向论文; 工况论文; 应力论文; 体系论文; 《建筑模拟》2020年第2期论文;