(潍坊学院数学与信息科学学院,山东,潍坊, 261061)
摘要:针对几种特殊形式的分配问题,通过实例来讨论其具体的求解方法,本文的方法丰富了已有的内容,具有较高的实际应用价值.
关键词:分配问题;匈牙利法;不平衡;
中图分类号:O221 文献标识码:A
0 引言
在生产生活中常常遇到分配问题,比如在学校运动会时,如何挑选5名同学去参加5个体育项目的比赛,以使得比赛总成绩最好,或者如何将4项工作分配给4个工作人员去完成,使得完成这4项工作的总时间最短等.分配问题最经典的求解方法是匈牙利法[1],现在很多学者都对分配问题及其解法做了详细的研究[2]-[4],本文主要针对几种特殊形式的分配问题进行研究.
1 平衡分配问题

第一个约束条件表示每人只能做一项工作,第二个约束条件表示每项工作只能由一人完成,效率矩阵为n阶方阵.平衡分配问题可以通过已有的匈牙利方法求解,其余特殊形式的分配问题都需要转化为平衡分配问题来考虑.
2 不平衡分配问题
不平衡分配问题是指所要完成的工作数m和人数n不相等的情况,在实际中可能是工作数大于人数,也可能是工作数小于人数,对于这类问题,又可以具体分两种情况讨论.
(1)每人只能做一项工作,每项工作只能由一人完成
当工作数m大于人数n时(m>n),效率矩阵为n×m的矩阵,此时需要虚设工作人员,个数为m-n,将其修改为平衡分配问题,具体计算时需要在效率矩阵中加入m-n行0,将效率矩阵变为方阵再利用匈牙利方法计算,效率为0表示虚设的人员在实际中并没有进行工作.
当工作数m小于人数n时(m<n),此时需要虚设工作,个数为n - m,需要在效率矩阵中加入m-n列0,将效率矩阵变为方阵再利用匈牙利方法计算,添加0实际上表示该工作没有工作人员来完成.
(2)每人或者某人可以同时做多项工作
在这种情况下,同样需要进行虚设相应的工作或者人员,但是效率矩阵中添加的行或列就需要由具体的情况来讨论而不能单纯的按照(1)中添加0来完成.
3 某人不能做某项工作的分配问题
在实际的分配任务时,可能存在这样的情况,某个工作人员不能进行某一项工作的操作,或者某项工作不能交给其中的某人来完成,在这种情况下,需要将对应位置的cij设为M(M为任意大的正数),表示不能进行相关工作分配,否则损失惨重.
下面针对具体的问题举例讨论.
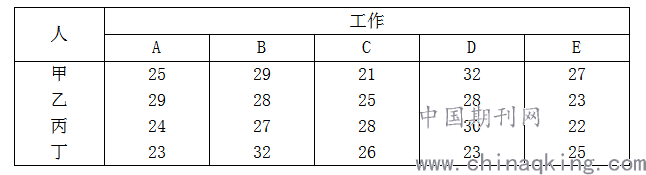
例 现有A、B、C、D、E五项工作,要分配给甲、乙、丙、丁四人完成,每人完成任务的时间如表1所示,有如下考虑:
1)工作A必须完成,其余4项中可以选择3项完成;
2)规定所有的工作必须完成,故有一人要完成两项,其余每人完成一项;
3)工作B由乙或者丙完成,工作C由丙或丁完成,工作E由甲、乙或丙完成,并且规定四人中乙或者丙完成两项工作,其余每人完成一项工作;
试分别确定各自的最优分配方案,使完成所有工作的总时间最少.
表1 工作时间(单位:h)
解:因为本题中有四个工作人员,五项工作,属于不平衡分配问题,故需要虚设一人戊.
1)因为A必须完成,所以A不能由虚设的戊完成,其余工作可以,因此效率表为
表2 工作时间(单位:h)
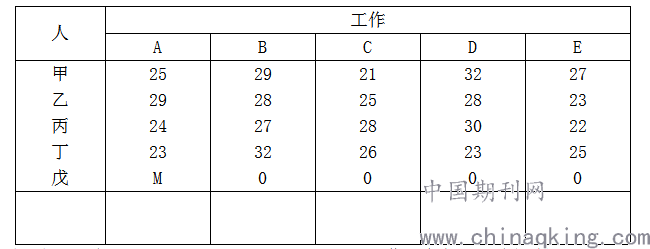
解此分配问题,得甲—C,乙—E,丙—A,丁—D,B工作没有完成,最小时间91h.
2)由于没有具体说明哪个人完成两项工作,所以戊完成各项工作的时间应为四人完成本项工作的最小时间,因此该问题的效率表为
表3 工作时间(单位:h)
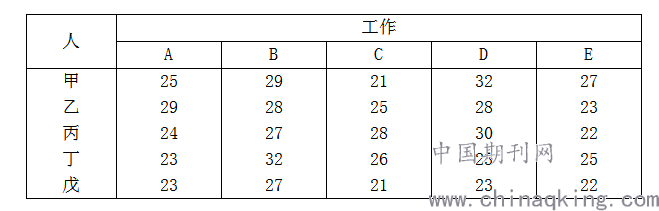
解此分配问题,得甲—C,乙—E,丙—B,丁—A,D,或者甲—C,乙—B,丙—E,丁—A,D,最小时间117h.
3)此问题的效率表为
表1 时间表
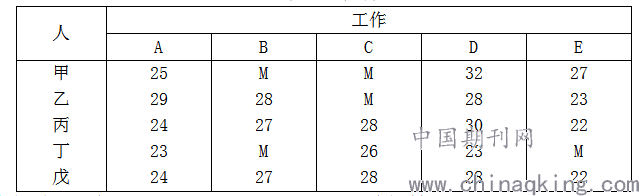
参考文献:
[1] 胡运权.运筹学(第六版)[M].北京:高等教育出版社,2014.2.
[2] 刘树立,于丽英. 人数与任务数不相等的指派问题[J].运筹与管理,2005,14(2),64-66.
[3] 苏祥定等.不平衡指派问题的差额法求解及其应用[J].计算机工程,2005,12(22):178-180.
[4] 杜金玲,周杰.关于几种不平衡指派问题的修正匈牙利求解[J],价值工程,2010, 19(13),120-122.
论文作者:潘爱霞
论文发表刊物:《未来教育家》2019年第11期
论文发表时间:2019/12/18
标签:工作论文; 分配论文; 匈牙利论文; 矩阵论文; 效率论文; 不平衡论文; 时间论文; 《未来教育家》2019年第11期论文;
